题目内容
已知α为钝角,且sinα=
,则与角α终边相同的角β的集合为
| 1 |
| 2 |
{β|β=
+2kπ,k∈Z}
| 5π |
| 6 |
{β|β=
+2kπ,k∈Z}
.| 5π |
| 6 |
分析:根据正弦函数的图象,求出所有满足sinα=
的角α,再根据α为钝角可得α=
,结合任意角的定义即可写出与角α终边相同的角β的集合.
| 1 |
| 2 |
| 5π |
| 6 |
解答:解:∵sinα=
,∴α=
+2kπ或α=
+2kπ(k∈Z).
又∵α为钝角,∴α=
.
∵角β与角α终边相同,
∴角β的集合为{β|β=
+2kπ,k∈Z}.
故答案为:{β|β=
+2kπ,k∈Z}
| 1 |
| 2 |
| π |
| 6 |
| 5π |
| 6 |
又∵α为钝角,∴α=
| 5π |
| 6 |
∵角β与角α终边相同,
∴角β的集合为{β|β=
| 5π |
| 6 |
故答案为:{β|β=
| 5π |
| 6 |
点评:本题给出钝角α的正弦之值,求与角α终边相同的角β的集合,着重考查了特殊角的三角函数值、终边相同的角的集合等知识,属于基础题.

练习册系列答案
相关题目
已知α为钝角,且sin(α+
)=
,则cos(α+
)的值为( )
| π |
| 12 |
| 1 |
| 3 |
| 5π |
| 12 |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、
|
 )=
)= ,则cos(α+
,则cos(α+ )的值为
)的值为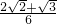


 )=
)= ,则cos(α+
,则cos(α+ )的值为( )
)的值为( )


