题目内容
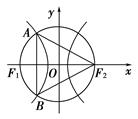
如图所示,F1和F2分别是双曲线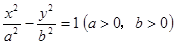 的两个焦点,A和B是以O为圆心,|OF1|为半径的圆与该双曲线左支的两个交点,且△F2AB是等边三角形,则离心率为( )
的两个焦点,A和B是以O为圆心,|OF1|为半径的圆与该双曲线左支的两个交点,且△F2AB是等边三角形,则离心率为( )
A. | B.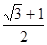 | C.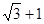 | D. |
C
解析试题分析:连接AF1,根据△F2AB是等边三角形可知∠AF2B=60°,F1F2是圆的直径可表示出|AF1|、|AF2|,再由双曲线的定义可得 c-c=2a,从而可求双曲线的离心率.
c-c=2a,从而可求双曲线的离心率.
连接AF1,则∠F1AF2=90°,∠AF2B=60°
∴|AF1|=c,|AF2|= c,∴
c,∴ c-c=2a,∴e=
c-c=2a,∴e= =
=
 ,故选C.
,故选C.
考点:本题主要考查双曲线的简单性质.考查了学生综合分析问题和数形结合的思想的运用.属基础题
点评:解决该试题的关键是根据双曲线的定义以及等边三角形的性质得到关于a,b,c的关系式,进而得到其离心率的求解。

练习册系列答案
相关题目
已知点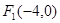 和
和 ,曲线上的动点P到
,曲线上的动点P到 、
、 的距离之差为6,则曲线方程为()
的距离之差为6,则曲线方程为()
A. | B.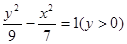 |
C. 或 或 | D. |
已知实数x、y满足2x+y+5=0,那么 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
椭圆 上一点P到两焦点的距离之积为m,则m取最大值时P点坐标是( )
上一点P到两焦点的距离之积为m,则m取最大值时P点坐标是( )
| A.(0,3)或(0,-3) | B.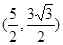 或 或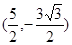 |
| C.(5,0)或(-5,0) | D. 或 或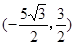 |
双曲线两条渐近线互相垂直,那么它的离心率为 ( )
| A.2 | B.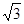 | C.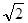 | D.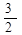 |
设P是双曲线 与圆
与圆 在第一象限的交点,
在第一象限的交点, 分别是双曲线的左右焦点,且
分别是双曲线的左右焦点,且 则双曲线的离心率为( )
则双曲线的离心率为( )
A. | B. | C.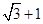 | D.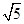 |




 ,
, 、
、 分别是它的左、右焦点,若过
分别是它的左、右焦点,若过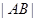 是
是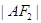 与
与 的等差中项,则
的等差中项,则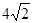

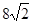
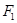 和
和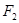 为双曲线
为双曲线
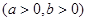 的两个焦点, 若
的两个焦点, 若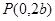 是正三角形的三个顶点,则双曲线的离心率为 ( )
是正三角形的三个顶点,则双曲线的离心率为 ( )