题目内容
(本小题满分12分)已知函数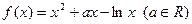 .
.
(I)若函数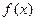 在
在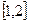 上是减函数,求实数
上是减函数,求实数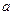 的取值范围;
的取值范围;
(II)令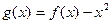 ,是否存在实数
,是否存在实数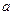 ,使得当
,使得当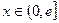 时,函数
时,函数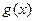 的最小值是
的最小值是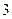 ,若存在,求出实数
,若存在,求出实数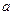 的值,若不存在,说明理由?
的值,若不存在,说明理由?
(III)当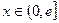 时,证明:
时,证明: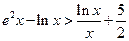 .
.
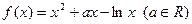 .
.(I)若函数
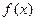 在
在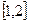 上是减函数,求实数
上是减函数,求实数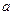 的取值范围;
的取值范围;(II)令
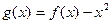 ,是否存在实数
,是否存在实数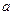 ,使得当
,使得当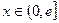 时,函数
时,函数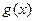 的最小值是
的最小值是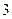 ,若存在,求出实数
,若存在,求出实数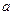 的值,若不存在,说明理由?
的值,若不存在,说明理由?(III)当
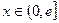 时,证明:
时,证明: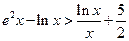 .
.(1)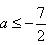 (2)
(2) (3)略
(3)略
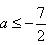 (2)
(2) (3)略
(3)略(I)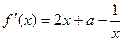 …………………………………1分
…………………………………1分
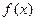 在
在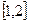 上单调递减,因此当
上单调递减,因此当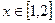 时,
时,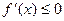 恒成立
恒成立
即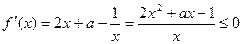 ,化简得
,化简得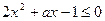 (
(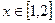 )
)
令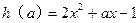 ,即
,即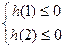 ,
, ………………………………4分
………………………………4分
(II)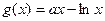 ,
,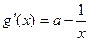 …………………………………5分
…………………………………5分
当 时
时
 ,
,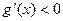 ,
,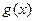 单调递减;
单调递减;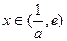 ,
,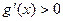 ,
,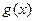 单调递增;
单调递增;
 ,
,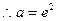
当 时,
时, ,
,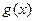 单调递减,
单调递减,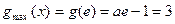 ,
,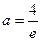 (舍)
(舍)
综上 ………………………………8分
………………………………8分
(III)由(II)可知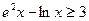
令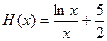 ,
,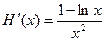 , …………………………………9分
, …………………………………9分
当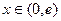 时,
时, ,
,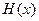 单调递增,
单调递增,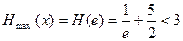
即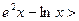
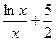 恒成立 …………………………………12分
恒成立 …………………………………12分
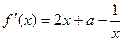 …………………………………1分
…………………………………1分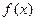 在
在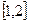 上单调递减,因此当
上单调递减,因此当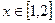 时,
时,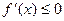 恒成立
恒成立即
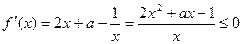 ,化简得
,化简得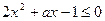 (
(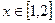 )
)令
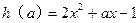 ,即
,即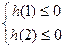 ,
, ………………………………4分
………………………………4分(II)
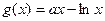 ,
,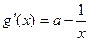 …………………………………5分
…………………………………5分当
 时
时 ,
,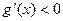 ,
,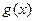 单调递减;
单调递减;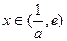 ,
,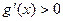 ,
,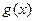 单调递增;
单调递增; ,
,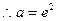
当
 时,
时, ,
,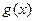 单调递减,
单调递减,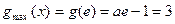 ,
,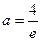 (舍)
(舍)综上
 ………………………………8分
………………………………8分(III)由(II)可知
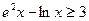
令
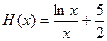 ,
,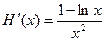 , …………………………………9分
, …………………………………9分当
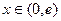 时,
时, ,
,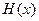 单调递增,
单调递增,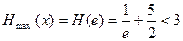
即
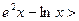
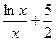 恒成立 …………………………………12分
恒成立 …………………………………12分
练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
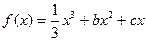 (b、c为常数)的两个极值点分别为
(b、c为常数)的两个极值点分别为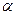 、
、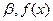 在点
在点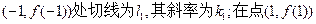 处的切线为l2,其斜率为k2。
处的切线为l2,其斜率为k2。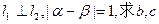 ;
;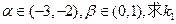 的取值范围。
的取值范围。
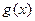 的单调递增区间;
的单调递增区间;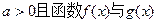 的图像有公共点,且在该点处的切线相同,用a表示b,并求b的最大值。
的图像有公共点,且在该点处的切线相同,用a表示b,并求b的最大值。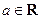 ,函数
,函数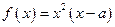 .
.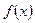 在区间
在区间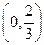 内是减函数,求实数
内是减函数,求实数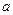 的取值范围;
的取值范围;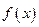 在区间
在区间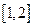 上的最小值
上的最小值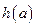 ;
;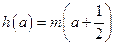 有两个不相等的实数解,求实数
有两个不相等的实数解,求实数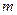 的取值范围.
的取值范围.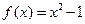 与函数
与函数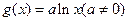 .
.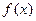 ,
,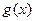 的图像在点
的图像在点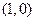 处有公共的切线,求实数
处有公共的切线,求实数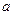 的值;
的值;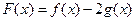 ,求函数
,求函数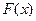 的值.
的值.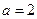 ,求过点
,求过点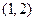 处的切线方程;
处的切线方程;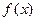 是否为“Storm函数”?如果是,请给出证明;如果不是,请说明理由.
是否为“Storm函数”?如果是,请给出证明;如果不是,请说明理由. =6,则x0=( )
=6,则x0=( )



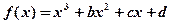 (b,c,d为常数),当
(b,c,d为常数),当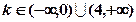 时,
时,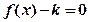 只有一个实数根;当
只有一个实数根;当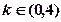 时,
时,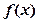 有2个极值点; ②
有2个极值点; ②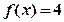 和
和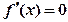 有一个相同的实根;
有一个相同的实根;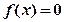 和
和 是
是 的导函数,则
的导函数,则 的值是 .
的值是 .