题目内容
(本小题满分14分)已知
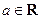 ,函数
,函数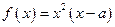 .
.(1)若函数
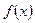 在区间
在区间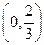 内是减函数,求实数
内是减函数,求实数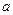 的取值范围;
的取值范围;(2)求函数
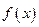 在区间
在区间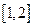 上的最小值
上的最小值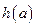 ;
;(3)对(2)中的
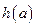 ,若关于
,若关于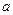 的方程
的方程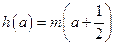 有两个不相等的实数解,求实数
有两个不相等的实数解,求实数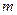 的取值范围.
的取值范围.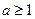 ,
,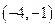
解:(1)∵
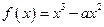 ,∴
,∴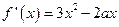 .……………………1分
.……………………1分∵函数
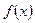 在区间
在区间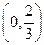 内是减函数,∴
内是减函数,∴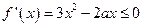 在
在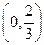 上恒成立. 2分
上恒成立. 2分即
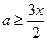 在
在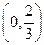 上恒成立,…………………………………………………3分
上恒成立,…………………………………………………3分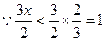 ,∴
,∴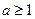 .
.故实数
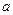 的取值范围为
的取值范围为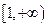 .……………………………………………………4分
.……………………………………………………4分(2)∵
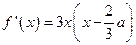 ,令
,令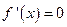 得
得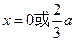 .………………5分
.………………5分①若
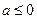 ,则当
,则当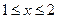 时,
时,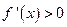 ,所以
,所以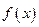 在区间
在区间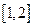 上是增函数,
上是增函数,所以
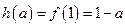 .………………………………………………………………6分
.………………………………………………………………6分②若
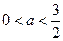 ,即
,即 ,则当
,则当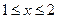 时,
时,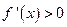 ,所以
,所以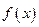 在区间
在区间
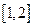 上是增函数,所以
上是增函数,所以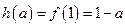 .……………………………………………………………7分
.……………………………………………………………7分③若
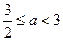 ,即
,即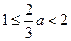 ,则当
,则当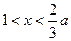 时,
时,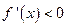 ;当
;当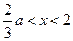 时,
时,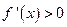 .
.所以
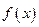 在区间
在区间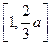 上是减函数,在区间
上是减函数,在区间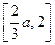 上是增函数.
上是增函数.所以
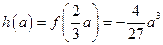 .…………………………………………………………8分
.…………………………………………………………8分④若
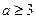 ,即
,即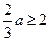 ,则当
,则当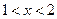 时,
时,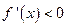 ,所以
,所以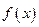 在区间
在区间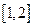 上是减函数.
上是减函数.
所以
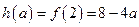 .………………………………………………………………9分
.………………………………………………………………9分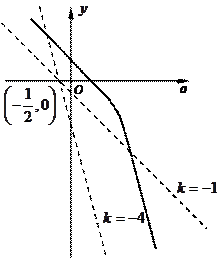 综上所述,函数
综上所述,函数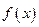 在区间
在区间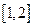 的最小值
的最小值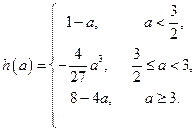 …10分
…10分(3)由题意
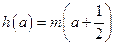 有两个不相等的实数解,
有两个不相等的实数解,即
(2)中函数
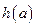 的图像与直线
的图像与直线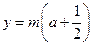 有两个
有两个不同的交点.…………………………………………………………11分
而直线
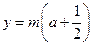 恒过定点
恒过定点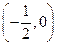 ,
,由右图知实数
 的取值范围是
的取值范围是 .…………………………14分
.…………………………14分
练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 且
且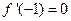
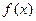 的单调区间;
的单调区间; 

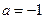 ,设函数
,设函数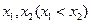 处取得极值
处取得极值 ,记点
,记点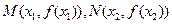 ,证明:线段
,证明:线段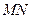 与曲线
与曲线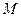 、
、
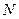 的公共点;
的公共点;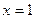 是函数
是函数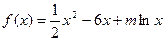 的一个极值点。
的一个极值点。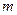 ;
;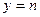 与函数
与函数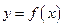 的图象有3个交点,求
的图象有3个交点,求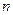 的取值范围;
的取值范围;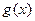 =(
=(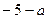 )
)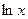 +
+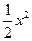 +(6-
+(6-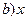 +2(
+2(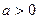 ),
),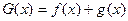 ,若
,若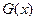 =0有两个零点
=0有两个零点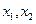 ,且
,且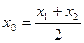 ,试探究
,试探究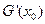 值的符号
值的符号
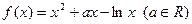 .
.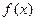 在
在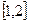 上是减函数,求实数
上是减函数,求实数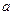 的取值范围;
的取值范围;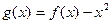 ,是否存在实数
,是否存在实数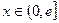 时,函数
时,函数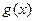 的最小值是
的最小值是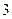 ,若存在,求出实数
,若存在,求出实数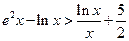 .
.
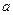 =1时,判断函数
=1时,判断函数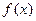 的单调性并写出其单调区间;
的单调性并写出其单调区间;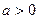 的条件下,若函数
的条件下,若函数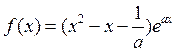 (
(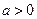 )
)
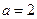 时,求函数
时,求函数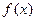 的单调区间;
的单调区间;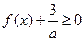 对
对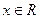 恒成立,求a的取值范围
恒成立,求a的取值范围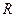 上的函数
上的函数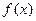 满足
满足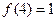 ,
,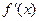 为
为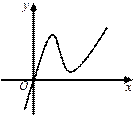
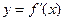 的图像如右图所示,
的图像如右图所示,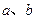 满足
满足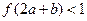 ,则
,则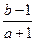 的取值范围是 .
的取值范围是 .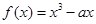 (
(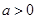 )的零点都在区间[-10,10]上,则使得方程
)的零点都在区间[-10,10]上,则使得方程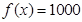 有正整数解的实数
有正整数解的实数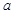 的取值个数为 ( )
的取值个数为 ( ) =__________.
=__________.