题目内容
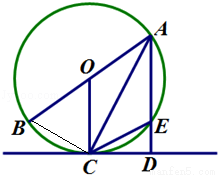
(10分)如图,已知AB是⊙O的直径,CD是⊙O的切线,C为切点,连接AC,过点A作AD⊥CD于点D,交⊙O于点E.

(Ⅰ)证明:∠AOC=2∠ACD;(Ⅱ)证明:ABCD=ACCE.
详见解析.
【解析】
试题分析:(Ⅰ)连结BC,∵CD是⊙O的切线,C为切点,由弦切角定理知∠ACD=∠ABC,
因为∠AOC是三角形OBC的外角,要证∠AOC=2∠ACD,只要证∠OCB=∠ABC;
(Ⅱ)要证ABCD=ACCE,只需证 ,只要证Rt△ABC∽Rt△CED,所以只要利用圆周角和弦切角证明∠OAC=∠OCA=∠CAE=∠ECD即可.
,只要证Rt△ABC∽Rt△CED,所以只要利用圆周角和弦切角证明∠OAC=∠OCA=∠CAE=∠ECD即可.
试题解析: 证明:(Ⅰ)连结BC,∵CD是⊙O的切线,C为切点,
∴∠ACD=∠ABC,
∵OB=OC,∴∠OCB=∠ABC,
又∵∠AOC=∠OCB+∠OBC,
∴∠AOC=2∠AC D.
(Ⅱ)∵AB是⊙O的直径,∴∠ACB=90°,
又∵AD⊥CD于D,∴∠ADC=90°,
∵CD是⊙O的切线,C为切点,OC为半径,
∴∠OAC=∠CAE,且OC⊥CD,
∴OC∥AD,又∵OC=OA,
∴∠OAC=∠OCA=∠CAE=∠ECD,
∴Rt△ABC∽Rt△CED,∴ ,
,
∴ABCD=ACCE.
考点:1、圆周角;2、弦切角.

练习册系列答案
相关题目
 长轴的端点为
长轴的端点为 、
、 ,且椭圆上的点到焦点的最小距离是
,且椭圆上的点到焦点的最小距离是 .
. 的标准方程;
的标准方程; 为原点,
为原点, 是椭圆
是椭圆 上异于
上异于 、
、 的任意一点,直线
的任意一点,直线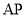 ,
, 分别交
分别交 轴于
轴于 ,
, ,问
,问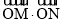 是否为定值,说明理由.
是否为定值,说明理由. 的定义域为( )
的定义域为( ) B.
B. C.
C. D.
D.
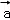 ,
, 满足|
满足| +
+ |=
|=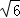 ,|
,| B.
B.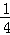 C.
C.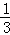 D.
D.
 则
则 的值为____________.
的值为____________. ,
, ,则
,则 的最小值是 .
的最小值是 .