题目内容
(10分)设数列{an}是公比为正数的等比数列,a1=2,a3﹣a2=12.
(1)求数列{an}的通项公式;
(2)设数列{bn}是首项为1,公差为2的等差数列,求数列{an+bn}的前n项和Sn.
(1) ;(2)
;(2)
【解析】
试题分析:(1)设出等比数列 的公比
的公比 ,利用条件a1=2,a3﹣a2=12列方程组,求出公比
,利用条件a1=2,a3﹣a2=12列方程组,求出公比 的值,进而得到数列的通项公式;
的值,进而得到数列的通项公式;
(2)数列{an+bn}是由一个等差数列和一个等比数列对应项相加得来的,所以可以采用拆项分组的方法,转化为等差数列、等比数列的前n项和问题来解决.
试题解析:【解析】
(1)设数列{an}的公比为q,由a1=2,a3﹣a2=12,
得:2q2﹣2q﹣12=0,即q2﹣q﹣6=0.
解得q=3或q=﹣2,
∵q>0,
∴q=﹣2不合题意,舍去,故q=3.
∴an=2×3n﹣1;
(2)∵数列{bn}是首项b1=1,公差d=2的等差数列,
∴bn=2n﹣1,
∴Sn=(a1+a2+ +an)+(b1+b2+ +bn)
= +
+
=3n﹣1+n2.
考点:等差数列与等比数列.

练习册系列答案
相关题目
 的递减区间为 .
的递减区间为 .

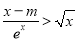 成立,则实数m的取值范围为( )
成立,则实数m的取值范围为( )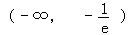
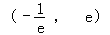

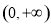
 的是 ( )
的是 ( ) 
 ,
,


 则目标函数
则目标函数 的取值范围是
的取值范围是 B.
B. C.
C. D.
D.