题目内容
已知函数f(x)=x3+ax2﹣9x+1,下列结论中错误的是( )
A.x0∈R,f(x0)=0
B.“a=3”是“﹣3为f(x)的极大值点”的充分不必要条件
C.若x0是f(x)的极小值点,则f(x)在区间(x0,+∞)单调递增
D.若3是f(x)的极值点,则f(x)的单调递减区间是(﹣1,3)
B
【解析】
试题分析:因为 ,所以
,所以
令 ,即
,即 ,
,
因为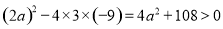 ,所以方程
,所以方程 有两个不相等的实数根,设这两个根为
有两个不相等的实数根,设这两个根为 且
且 ,且
,且 ;
;
当 或
或 时,
时, ;当
;当 时,
时,
所以函数 在区间
在区间 和
和 上都是增函数,在区间
上都是增函数,在区间 上为减函数,在
上为减函数,在 处取得极大值,在
处取得极大值,在 处取有极小值.函数的值域为R.
处取有极小值.函数的值域为R.
所以选项A正确;
当“ ”时,
”时, ,所以“﹣3为f(x)的极大值点”;
,所以“﹣3为f(x)的极大值点”;
反过来,若“﹣3为f(x)的极大值点”,则 是方程
是方程 的一个根,由韦达定理知,另一根为
的一个根,由韦达定理知,另一根为 ,所以“﹣3为f(x)的极大值点”,所以“a=3”是“﹣3为f(x)的极大值点”的充必要条件;所以选项B不正确;选项C、D均正确,综上只有B项不正确.
,所以“﹣3为f(x)的极大值点”,所以“a=3”是“﹣3为f(x)的极大值点”的充必要条件;所以选项B不正确;选项C、D均正确,综上只有B项不正确.
故选B.
考点:导数在研究函数性质中的应用.

练习册系列答案
相关题目
 满足
满足 ,则下列不等式成立的是( ).
,则下列不等式成立的是( ). B.
B. C.
C. D.
D.
 的递减区间为 .
的递减区间为 .
 ,则z=x+2y的最大值为 _________ .
,则z=x+2y的最大值为 _________ .
 在点(0,1)处的切线的斜率是
在点(0,1)处的切线的斜率是  B.
B. C.2 D.1
C.2 D.1