题目内容
已知直线l:y=2x- 与椭圆C:
与椭圆C: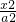 +y2=1 (a>1)交于P、Q两点,
+y2=1 (a>1)交于P、Q两点,
(1)设PQ中点M(x0,y0),求证:x0< ;
;
(2)以PQ为直径的圆过椭圆C的右顶点A.求椭圆C的方程.
解:(1)证明:把y=2x- 代入
代入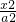 +y2=1 (a>1),
+y2=1 (a>1),
得: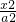 +(2x-
+(2x- )2=1(a>1),
)2=1(a>1),
整理,得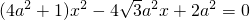 ,
,
∴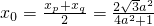 ,
,
∵4a2+1>4a2,
∴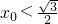 .
.
(2)由题设知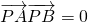 ,
,
∴(xp-a)(xq-a)+ypyq=0,
∵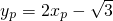 ,
,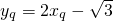 ,
,
∴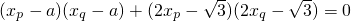 ,
,
由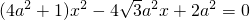 ,
,
知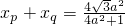 ,
,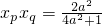 ,
,
∴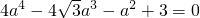 ,
,
即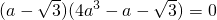 ,
,
∵a>1,
∴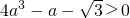 ,故a=
,故a= .
.
∴椭圆C的方程 .
.
分析:(1)把y=2x- 代入
代入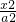 +y2=1 (a>1),得
+y2=1 (a>1),得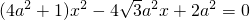 ,
,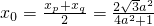 ,mh 4a2+1>4a2,能够证明
,mh 4a2+1>4a2,能够证明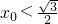 .
.
(2)由题设知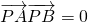 ,(xp-a)(xq-a)+ypyq=0,所以
,(xp-a)(xq-a)+ypyq=0,所以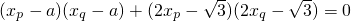 ,即
,即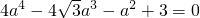 ,由a>1,得
,由a>1,得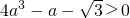 ,故a=
,故a= .由此能求出椭圆C的方程.
.由此能求出椭圆C的方程.
点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系,椭圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.
 代入
代入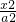 +y2=1 (a>1),
+y2=1 (a>1),得:
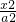 +(2x-
+(2x- )2=1(a>1),
)2=1(a>1),整理,得
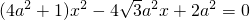 ,
,∴
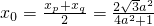 ,
,∵4a2+1>4a2,
∴
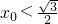 .
.(2)由题设知
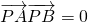 ,
,∴(xp-a)(xq-a)+ypyq=0,
∵
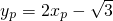 ,
,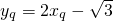 ,
,∴
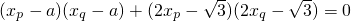 ,
,由
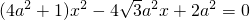 ,
,知
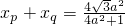 ,
,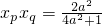 ,
,∴
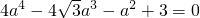 ,
,即
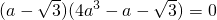 ,
,∵a>1,
∴
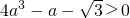 ,故a=
,故a= .
.∴椭圆C的方程
 .
.分析:(1)把y=2x-
 代入
代入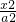 +y2=1 (a>1),得
+y2=1 (a>1),得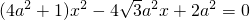 ,
,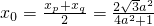 ,mh 4a2+1>4a2,能够证明
,mh 4a2+1>4a2,能够证明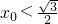 .
.(2)由题设知
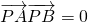 ,(xp-a)(xq-a)+ypyq=0,所以
,(xp-a)(xq-a)+ypyq=0,所以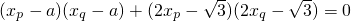 ,即
,即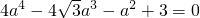 ,由a>1,得
,由a>1,得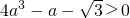 ,故a=
,故a= .由此能求出椭圆C的方程.
.由此能求出椭圆C的方程.点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系,椭圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.

练习册系列答案
相关题目