题目内容
5. 如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=$\frac{1}{2}$AD,∠BAD=∠ABC=90°,E是PD的中点.
如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=$\frac{1}{2}$AD,∠BAD=∠ABC=90°,E是PD的中点.(Ⅰ)证明:直线CE∥平面PAB;
(Ⅱ)点M为棱PC 的中点,求二面角M-AB-D的余弦值.
分析 (Ⅰ)取PA的中点F,连接EF,BF,只需证明BCEF是平行四边形,可得CE∥BF,即可得直线CE∥平面PAB;
(Ⅱ) 取AD的中点O,M在底面ABCD上的射影N为OC的中点.
取AB的中点Q,连接MQ,NQ,即可得∠MQN就是二面角M-AB-D的平面角,解直角三角形MNQ即可得二面角M-AB-D的余弦值
解答 解(Ⅰ)证明:取PA的中点F,连接EF,BF,因为E是PD的中点,
所以EF∥AD且EF=AD,AB=BC=$\frac{1}{2}$AD,∠BAD=∠ABC=90°,∴BC∥$\frac{1}{2}$AD,
∴BCEF是平行四边形,可得CE∥BF,BF?平面PAB,CF?平面PAB,
∴直线CE∥平面PAB;
(Ⅱ)解:四棱锥P-ABCD中,
侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=$\frac{1}{2}$AD,
∠BAD=∠ABC=90°,E是PD的中点.
取AD的中点O,M在底面ABCD上的射影N为OC的中点.
取AB的中点Q,连接MQ,NQ
设AD=2,则AB=BC=1,OP=$\sqrt{3}$,
所以∠MQN就是二面角M-AB-D的平面角.
由在直角三角形MNQ中,$MN=\frac{1}{2}PO=\frac{{\sqrt{3}}}{2},NQ=1,MQ=\sqrt{{1^2}+{{({\frac{{\sqrt{3}}}{2}})}^2}}=\frac{{\sqrt{7}}}{2}$
二面角M-AB-D的余弦值为:$\frac{NQ}{MQ}=\frac{1}{{\frac{{\sqrt{7}}}{2}}}=\frac{{2\sqrt{7}}}{7}$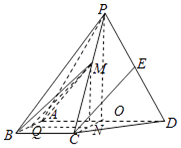
点评 本题考查了线面平行的判定,几何法求二面角,属于中档题.

练习册系列答案
相关题目
15.之前国家统计局公布了《2013年农民工监测调查报告》,报告显示:我国农民工收入持续快速增长.某地区农民工人均月收入增长率如图1,并将人均月收入绘制成如图2的不完整的条形统计图.根据以上统计图来判断以下说法错误的是( )


| A. | 2013年农民工人均月收入的增长率是10% | |
| B. | 2011年农民工人均月收入是2205元 | |
| C. | 2009年到2013年这五年中2013年农民工人均月收入最高 | |
| D. | 小明看了统计图后说:“农民工2012年的人均月收入比2011年的少了” |
16.已知全集为R,集合A={x|y=log2(1-2-x)},B={x|y=$\sqrt{-{x}^{2}+6x-8}$},则A∩∁RB=( )
| A. | {x|x≤0} | B. | {x|2≤x≤4} | C. | {x|0<x<2或x>4} | D. | {x|0<x≤2或x≥4} |
20.共享单车是指企业在校园、地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车单车共享服务,是共享经济的一种新形态.一个共享单车企业在某个城市就“一天中一辆单车的平均成本(单位:元)与租用单车的数量(单位:千辆)之间的关系”进行调查研究,在调查过程中进行了统计,得出相关数据见下表:
根据以上数据,研究人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲:$\stackrel{∧}{y}$(1)=$\frac{4}{x}$+1.1,方程乙:$\stackrel{∧}{y}$(2)=$\frac{6.4}{{x}^{2}}$+1.6.
(1)为了评价两种模型的拟合效果,完成以下任务:
①完成下表(计算结果精确到0.1)(备注:$\stackrel{∧}{{e}_{i}}$=yi-$\stackrel{∧}{{y}_{i}}$,$\stackrel{∧}{{e}_{i}}$称为相应于点(xi,yi)的残差(也叫随机误差);
②分别计算模型甲与模型乙的残差平方和Q1及Q2,并通过比较Q1,Q2的大小,判断哪个模型拟合效果更好.
(2)这个公司在该城市投放共享单车后,受到广大市民的热烈欢迎,共享单车常常供不应求,于是该公司研究是否增加投放.根据市场调查,这个城市投放8千辆时,该公司平均一辆单车一天能收入8.4元;投放1万辆时,该公司平均一辆单车一天能收入7.6元.问该公司应该投放8千辆还是1万辆能获得更多利润?(按(1)中拟合效果较好的模型计算一天中一辆单车的平均成本,利润=收入-成本).
| 租用单车数量x(千辆) | 2 | 3 | 4 | 5 | 8 |
| 每天一辆车平均成本y(元) | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
(1)为了评价两种模型的拟合效果,完成以下任务:
①完成下表(计算结果精确到0.1)(备注:$\stackrel{∧}{{e}_{i}}$=yi-$\stackrel{∧}{{y}_{i}}$,$\stackrel{∧}{{e}_{i}}$称为相应于点(xi,yi)的残差(也叫随机误差);
| 租用单车数量x(千辆) | 2 | 3 | 4 | 5 | 8 | |
| 每天一辆车平均成本y(元) | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
| 模型甲 | 估计值$\stackrel{∧}{{y}_{i}}$(1) | 2.4 | 2.1 | 1.6 | ||
| 残差$\stackrel{∧}{{e}_{i}}$(1) | 0 | -0.1 | 0.1 | |||
| 模型乙 | 估计值$\stackrel{∧}{{y}_{i}}$ (2) | 2.3 | 2 | 1.9 | ||
| 残差$\stackrel{∧}{{e}_{i}}$(2) | 0.1 | 0 | 0 | |||
(2)这个公司在该城市投放共享单车后,受到广大市民的热烈欢迎,共享单车常常供不应求,于是该公司研究是否增加投放.根据市场调查,这个城市投放8千辆时,该公司平均一辆单车一天能收入8.4元;投放1万辆时,该公司平均一辆单车一天能收入7.6元.问该公司应该投放8千辆还是1万辆能获得更多利润?(按(1)中拟合效果较好的模型计算一天中一辆单车的平均成本,利润=收入-成本).
9.设单位向量$\overrightarrow{e}$=(cos$α,\frac{1}{3}$),则cos2α的值为( )
| A. | $\frac{7}{9}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{7}{9}$ | D. | $\frac{\sqrt{3}}{2}$ |