题目内容
已知椭圆 ,点
,点 的坐标为
的坐标为 ,过点
,过点 的直线交椭圆
的直线交椭圆 于另一点
于另一点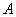 ,且
,且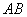 中点
中点 在直线
在直线 上,点
上,点 为椭圆
为椭圆 上异于
上异于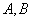 的任意一点。
的任意一点。
(1)求直线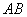 的方程,;
的方程,;
(2)设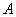 不为椭圆顶点,又直线
不为椭圆顶点,又直线 分别交直线
分别交直线 于
于 两点,证明:
两点,证明: 为定值.
为定值.
解:(1)若直线AB无斜率,直线方程x=0,A(0,1)满足要求
若直线AB有斜率,设直线方程y=kx-1,联立方程得
 ,
,
中点坐标为

 直线方程
直线方程 
 ,
, ,设点
,设点 为曲线上任一点
为曲线上任一点
直线 AP的方程是  与直线y=x联立得
与直线y=x联立得 
同理得:直线 BP的方程是  与直线y=x联立得
与直线y=x联立得 




练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 的图象,
的图象,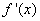 是函数
是函数 的解集为
的解集为 
 ,则
,则
 ,若方程
,若方程 恰有两个不同的实根时,则实数
恰有两个不同的实根时,则实数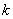 的取值范围是(其中
的取值范围是(其中 为自然对数的底数) ( ).
为自然对数的底数) ( ).




 ,其中
,其中 。如下说法中正确的有
。如下说法中正确的有  与
与 轴正方向的夹角恒为定值(即与
轴正方向的夹角恒为定值(即与 值无关);
值无关); 的最大值为
的最大值为 ;
; (
( 的夹角)的最大值为
的夹角)的最大值为 ;
; 的值可能为
的值可能为 ;
; ,则
,则 的最大值为
的最大值为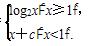 则“c=-1”是“函数f(x)在R上递增”的( )
则“c=-1”是“函数f(x)在R上递增”的( )