题目内容
若(x+1)n=xn+…+ax3+bx2+cx+1(n∈N*),且a:b=3:1,那么n= .
【答案】分析:根据条件中所给的二项式定理的展开式,写出a和b的值,根据这两个数字的比值,写出关于n的等式,即方程,解方程就可以求出n的值.
解答:解:∵(x+1)n=xn+…+ax3+bx2+cx+1(n∈N*),
∴a=Cn3,b=Cn2,
∵a:b=3:1,
∴a:b=Cn3:Cn2=3:1,
∴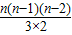 :
: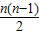 =3:1,
=3:1,
∴n=11.
故答案为:11
点评:本题是考查二项式定理应用,考查二项式定理的二项式系数,是一个基础题,解题的关键是写正确要用的a和b的值.
解答:解:∵(x+1)n=xn+…+ax3+bx2+cx+1(n∈N*),
∴a=Cn3,b=Cn2,
∵a:b=3:1,
∴a:b=Cn3:Cn2=3:1,
∴
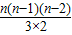 :
: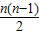 =3:1,
=3:1,∴n=11.
故答案为:11
点评:本题是考查二项式定理应用,考查二项式定理的二项式系数,是一个基础题,解题的关键是写正确要用的a和b的值.

练习册系列答案
相关题目