题目内容
(文)条件
下,函数p=log
(2x+y)的最小值为
(理)若(x+1)n=xn+…+ax3+bx2+…+1,(n∈N*),且a:b=3:1,则n=
|
| 2 |
| 5 |
-1
-1
.(理)若(x+1)n=xn+…+ax3+bx2+…+1,(n∈N*),且a:b=3:1,则n=
11
11
.分析:(文) 以为底的对数函数为减函数,利用线性规划知识先求出2x+y的最大值,再求p的最小值.
(理) 在(x+1)n 展开式中令x的指数分别为3,2,表示出a,b.代入并解即可.
(理) 在(x+1)n 展开式中令x的指数分别为3,2,表示出a,b.代入并解即可.
解答: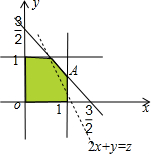 解:(文) 不等式表示的可行域如图设2x+y=z.变形为y=-2x+z,
解:(文) 不等式表示的可行域如图设2x+y=z.变形为y=-2x+z,
当直线l:y=-2x+z 经过点A(1,
)时,l在y轴上截距z最大,从而2x+y 最大,
此时z=2×1+
=
,∴函数p=log
(2x+y)的最小值为 log
=-1.
故答案为:-1
(理)(x+1)n展开式的通项为Cnrxn-r,
∴a:b=Cnn-3:Cnn-2=3:1,即 Cn3:Cn2=3:1,
:
=3:1.
解得n=11.
故答案为:11
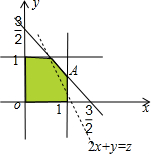 解:(文) 不等式表示的可行域如图设2x+y=z.变形为y=-2x+z,
解:(文) 不等式表示的可行域如图设2x+y=z.变形为y=-2x+z,当直线l:y=-2x+z 经过点A(1,
| 1 |
| ,2 |
此时z=2×1+
| 1 |
| 2 |
| 5 |
| 2 |
| 2 |
| 5 |
| 2 |
| 5 |
| 5 |
| 2 |
故答案为:-1
(理)(x+1)n展开式的通项为Cnrxn-r,
∴a:b=Cnn-3:Cnn-2=3:1,即 Cn3:Cn2=3:1,
| n(n-1)(n-2) |
| 6 |
| n(n-1) |
| 2 |
解得n=11.
故答案为:11
点评:(文)本题考查对数函数单调性,简单线性规划问题,数形结合的思想.属于基础题.
(理) 本题考查 二项式定理的简单直接应用,二项式系数的性质. 属于基础题.
(理) 本题考查 二项式定理的简单直接应用,二项式系数的性质. 属于基础题.

练习册系列答案
相关题目