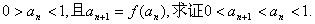题目内容
设 .
.
(1)当a=1时,求曲线y=f(x)在点(-1,f(-1))处的切线方程;
(2)当 时,求f(x)的极大值和极小值.
时,求f(x)的极大值和极小值.
解:(1)当a=1时,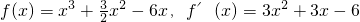
切线斜率
∴切点为(-1, )
)
∴切线为
(2)当 时,
时,
x<-2时,f′(x)>0;-2<x<3时,f′(x)<0;x>3时,f′(x)>0
∴x=-2时,f(x)的极大值为8,x=3时,f(x)的极小值为
分析:(1)当a=1时,先对函数求导,然后可求切线斜率 ,可求切线方程
,可求切线方程
(2)当 时,对函数求导,结合导数研究函数的单调性,进而可求函数的极大与极小值
时,对函数求导,结合导数研究函数的单调性,进而可求函数的极大与极小值
点评:本题主要考查了导数的基本应用:求解切线方程,求解函数的单调性,求解函数的极大与极小值
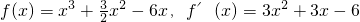
切线斜率

∴切点为(-1,
 )
)∴切线为

(2)当
 时,
时,
x<-2时,f′(x)>0;-2<x<3时,f′(x)<0;x>3时,f′(x)>0
∴x=-2时,f(x)的极大值为8,x=3时,f(x)的极小值为

分析:(1)当a=1时,先对函数求导,然后可求切线斜率
 ,可求切线方程
,可求切线方程(2)当
 时,对函数求导,结合导数研究函数的单调性,进而可求函数的极大与极小值
时,对函数求导,结合导数研究函数的单调性,进而可求函数的极大与极小值点评:本题主要考查了导数的基本应用:求解切线方程,求解函数的单调性,求解函数的极大与极小值

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
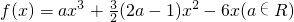
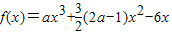 .
.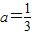 时,求f(x)的极大值和极小值.
时,求f(x)的极大值和极小值.
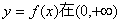 上是增函数;
上是增函数;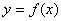 在
在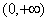 上是单调增函数,求正数a的范围;
上是单调增函数,求正数a的范围;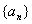 满足:
满足: