题目内容

10．过点F（0，2）且和直线y+2=0相切的动圆圆心的轨迹方程为（　　）
A．x2=8yB．y2=-8xC．y2=8xD．x2=-8y

分析 由已知条件可知：动圆圆心符合抛物线的定义，进而可求出．

解答 解：由题意，知动圆圆心到点F（0，2）的距离等于到定直线y=-2的距离，
故动圆圆心的轨迹是以F为焦点，直线y=-2为准线的抛物线，方程为x2=8y，
故选A．

点评 掌握抛物线的定义是解题的关键．

练习册系列答案
相关题目
20．从点A（2，-1，7）沿向量$\overrightarrow{a}$=（8，9，-12）的方向取线段长|AB|=34，则B点的坐标为（　　）
A．（18，17，-17）B．（-14，-19，17）C．$（{6，\frac{7}{2}，1}）$D．$（{-2，-\frac{11}{2}，13}）$
1．已知函数f（x）=ax-lnx，F（x）=ex+ax，其中x＞0，a＜0．
（1）若f（x）和F（x）在区间（0，ln3）上具有时间的单调性，求实数a的取值范围；
（2）若$a∈（{-∞，-\frac{1}{e^2}}]$，且函数g（x）=xeax-1-2ax+f（x）的最小值为φ（a），求φ（a）的最小值．
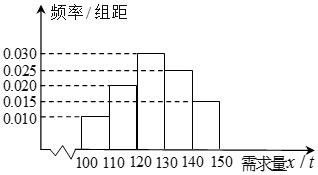18．随着经济模式的改变，微商和电商已成为当今城乡一种新型的购销平台．已知经销某种商品的电商在任何一个销售季度内，每售出1吨该商品可获利润0.5万元，未售出的商品，每1吨亏损.3万元．根据往年的销售经验，得到一个销售季度内市场需求量的频率分布直方图如右图所示．已知电商为下一个销售季度筹备了130吨该商品．现以x（单位：吨，100≤x≤150）表示下一个销售季度的市场需求量，T（单位：万元）表示该电商下一个销售季度内经销该商品获得的利润．
（Ⅰ）将T表示为x的函数，求出该函数表达式；
（Ⅱ）根据直方图估计利润T不少于57万元的概率；
（Ⅲ）根据频率分布直方图，估计一个销售季度内市场需求量x的平均数与中位数的大小．
5．函数f（x）=sinx+cosx的最小值为-$\sqrt{2}$．
15．△ABC的内角A、B、C的对边分别为a、b、c，满足：2cosC（acosB+bcosA）=c．
（1）求C；
（2）若a=2，△ABC的面积为$\frac{3\sqrt{3}}{2}$，求△ABC的周长．
2．已知sinα=-$\frac{3}{5}$，cosβ=1，则sin（α+β）=-$\frac{3}{5}$．
19．若不等式ax2+bx-2＞0的解集为（1，4），则a+b等于2．
20．在△ABC中，角A，B，C所对的边分别为a，b，c，且a，2b，c成等比数列，则cosB的最小值为（　　）
A．$\frac{1}{4}$B．$\frac{1}{3}$C．$\frac{1}{2}$D．$\frac{7}{8}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网