题目内容
已知a>b,二次三项式ax2 +2x +b≥0对于一切实数x恒成立,又 ,使
,使 成立,则
成立,则 的最小值为( )
的最小值为( )
| A.1 | B. | C.2 | D.2 |
D
解析试题分析:因为二次三项式ax2 +2x +b≥0对于一切实数x恒成立,所以 ;又
;又 ,使
,使 成立,所以
成立,所以 ,故只有
,故只有 ,即a>0,a>b,ab=1,所以
,即a>0,a>b,ab=1,所以 =a-b+
=a-b+ =
= ,故选D。
,故选D。
考点:本题主要考查二次函数恒成立问题,均值定理的应用,存在性命题。
点评:小综合题,较全面的考查二次函数恒成立问题,均值定理的应用及存在性命题的概念,从已知出发求得ab=1是解题的关键之一。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数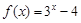 的零点所在区间为( )
的零点所在区间为( )
A.( 1,0) 1,0) | B.(0,1) | C.(1,2) | D.(2,3) |
若函数 满足
满足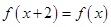 且
且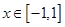 时,
时,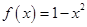 ,函数
,函数 ,则函数
,则函数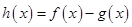 在区间
在区间 内的零点的个数为( )
内的零点的个数为( )
A. | B. | C. | D. |
已知函数 的图象如图所示(其中
的图象如图所示(其中 是函数
是函数 的导函数).下面四个图象中,
的导函数).下面四个图象中,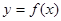 的图象大致是( )
的图象大致是( )

| A. | B. | C. | D. |
已知函数 ,正实数
,正实数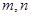 满足
满足 且
且 ,若
,若 在区间
在区间 上的最大值为2,则
上的最大值为2,则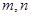 的值分别为
的值分别为
A. ,2 ,2 | B. , ,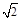 | C. ,2 ,2 | D. ,4 ,4 |
函数 的定义域为{0,1,2,3},那么其值域为( )
的定义域为{0,1,2,3},那么其值域为( )
A. | B.{0,1,2,3} |
C. | D. |


 上的任一点,若曲线在M点处的切线的倾斜角均不小于
上的任一点,若曲线在M点处的切线的倾斜角均不小于 的锐角,则实数a的取值范围是( )
的锐角,则实数a的取值范围是( )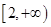



 满足以下三个条件:①对于任意的
满足以下三个条件:①对于任意的 ,都有
,都有 ;②对于任意的
;②对于任意的 ③函数
③函数 的图象关于y轴对称,则下列结论中正确的是
的图象关于y轴对称,则下列结论中正确的是


