题目内容
已知M是曲线 上的任一点,若曲线在M点处的切线的倾斜角均不小于
上的任一点,若曲线在M点处的切线的倾斜角均不小于 的锐角,则实数a的取值范围是( )
的锐角,则实数a的取值范围是( )
A.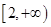 | B. | C. | D. |
C
解析试题分析:函数定义域为(0, ),曲线
),曲线 在M点处的切线的斜率,就是函数在此点的导数值。倾斜角均不小于
在M点处的切线的斜率,就是函数在此点的导数值。倾斜角均不小于 的锐角,所以斜率k满足
的锐角,所以斜率k满足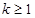 ,由K=
,由K=
 恒成立,且
恒成立,且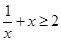 ,所以
,所以 ,故C。
,故C。
考点:本题主要考查导数的计算,导数的几何意义,三角函数性质,均值定理的应用。
点评:综合题,恒成立问题,往往要转化成求函数的最值,
本题由K=
 恒成立,转化得到
恒成立,转化得到 恒成立。
恒成立。

练习册系列答案
相关题目
已知函数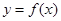 的周期为2,当
的周期为2,当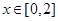 时,
时, ,如果
,如果
 ,则函数
,则函数 的所有零点之和为( )
的所有零点之和为( )
| A.2 | B.4 | C.6 | D.8 |
定义域是一切实数的函数 ,其图像是连续不断的,且存在常数
,其图像是连续不断的,且存在常数 (
( )
)
使得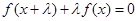 对任意实数
对任意实数 都成立,则称
都成立,则称 是一个“
是一个“ —伴随函数”. 有
—伴随函数”. 有
下列关于“ —伴随函数”的结论:
—伴随函数”的结论:
① 是常数函数中唯一一个“
是常数函数中唯一一个“ —伴随函数”;
—伴随函数”;
②“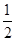 —伴随函数”至少有一个零点;
—伴随函数”至少有一个零点;
③ 是一个“
是一个“ —伴随函数”;
—伴随函数”;
其中正确结论的个数是 ( )
| A.1个; | B.2个; | C.3个; | D.0个; |
已知函数 ,若
,若 ,则
,则 等于 ( )
等于 ( )
A. | B. | C. | D. |
下列函数中,在其定义域内既是减函数又是奇函数为( )
A.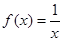 | B. |
C. | D. |
已知a>b,二次三项式ax2 +2x +b≥0对于一切实数x恒成立,又 ,使
,使 成立,则
成立,则 的最小值为( )
的最小值为( )
| A.1 | B. | C.2 | D.2 |
对于函数 和
和 ,其定义域为
,其定义域为  .若对于任意的
.若对于任意的 ,总有
,总有 则称
则称 可被
可被 置换,那么下列给出的函数中能置换
置换,那么下列给出的函数中能置换 的是 ( )
的是 ( )
A. | B.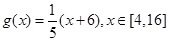 |
C.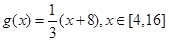 | D. |
若奇函数 在
在 上为增函数,且有最小值0,则它在
上为增函数,且有最小值0,则它在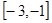 上( )
上( )
| A.是减函数,有最小值0 | B.是增函数,有最小值0 |
| C.是减函数,有最大值0 | D.是增函数,有最大值0 |
函数 的最大值为( )
的最大值为( )
A. | B. | C. | D. |