已知定义在R上的函数满足以下三个条件:①对于任意的.都有,②对于任意的③函数的图象关于y轴对称.则下列结论中正确的是A． B． C． D．题目和参考答案——青夏教育精英家教网—

题目内容

已知定义在R上的函数满足以下三个条件：①对于任意的，都有；②对于任意的③函数的图象关于y轴对称，则下列结论中正确的是

A．	B．
C．	D．

解析试题分析：因为对于任意的，都有，所以函数的周期4；因为对于任意的，所以函数在单调递增；因为函数的图象关于y轴对称，所以函数关于直线x=2对称，所以，所以。
考点：函数的周期性；函数的单调性；函数的对称性。
点评：函数的周期性是考试时的一个常考点，也是一个难点。因此我们在平常学习时要注意总结。

练习册系列答案

课课练与单元测试系列答案

相关题目

定义域是一切实数的函数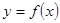，其图像是连续不断的，且存在常数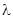(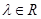)使得
对任意实数都成立，则称是一个“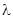—伴随函数”．有下列关于“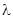—伴随函数”的结论：
①是常数函数中唯一一个“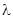—伴随函数”；
②“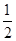—伴随函数”至少有一个零点；
③是一个“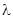—伴随函数”；
其中正确结论的个数是（）

已知a>b，二次三项式ax²+2x +b≥0对于一切实数x恒成立，又，使成立，则的最小值为（）

若是方程的解，则属于区间（　　）

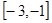若奇函数在上为增函数，且有最小值0，则它在上（）

A．是减函数，有最小值0	B．是增函数，有最小值0
C．是减函数，有最大值0	D．是增函数，有最大值0

下列四组函数中，表示相同函数的一组是（）

A．	B．
C．	D．

函数的图象大致是

设函数，曲线在点处的切线方程为，则曲线在点处切线的斜率为 ( )

已知函数为奇函数，则的值为（　　　）

试题分类