题目内容
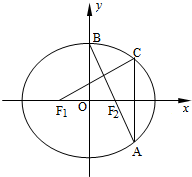 如图,在平面直角坐标系xOy中,F1,F2分别为椭圆
如图,在平面直角坐标系xOy中,F1,F2分别为椭圆| x2 |
| a2 |
| y2 |
| b2 |
(1)若点C的坐标为(
| 4 |
| 3 |
| 1 |
| 3 |
| 2 |
(2)若F1C⊥AB,求椭圆离心率e的值.
考点:椭圆的简单性质,椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(1)根据椭圆的定义,建立方程关系即可求出a,b的值.
(2)求出C的坐标,利用F1C⊥AB建立斜率之间的关系,解方程即可求出e的值.
(2)求出C的坐标,利用F1C⊥AB建立斜率之间的关系,解方程即可求出e的值.
解答:
解:(1)∵C的坐标为(
,
),
∴
+
=1,即
+
=9,
∵B
=b2+c2=a2,
∴a2=(
)2=2,即b2=1,
则椭圆的方程为
+y2=1.
(2)设F1(-c,0),F2(c,0),
∵B(0,b),
∴直线BF2:y=-
x+b,代入椭圆方程
+
=1(a>b>0)得(
+
)x2-
x=0,
解得x=0,或x=
,
∵A(
,
),且A,C关于x轴对称,
∴C(
,-
),
则kF1C=-
=
,
∵F1C⊥AB,
∴
•×(-
)=-1,
由b2=a2-c2得
=
,
即e=
.
| 4 |
| 3 |
| 1 |
| 3 |
∴
| ||
| a2 |
| ||
| b2 |
| 16 |
| a2 |
| 1 |
| b2 |
∵B
| F | 2 2 |
∴a2=(
| 2 |
则椭圆的方程为
| x2 |
| 2 |
(2)设F1(-c,0),F2(c,0),
∵B(0,b),
∴直线BF2:y=-
| b |
| c |
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| a2 |
| 1 |
| c2 |
| 2 |
| c |
解得x=0,或x=
| 2a2c |
| a2+c2 |
∵A(
| 2a2c |
| a2+c2 |
| b(c2-a2) |
| a2+c2 |
∴C(
| 2a2c |
| a2+c2 |
| b(c2-a2) |
| a2+c2 |
则kF1C=-
| ||
|
| a2b-bc2 |
| 3a2c+c3 |
∵F1C⊥AB,
∴
| b(a2-c2) |
| 3a2c+c3 |
| b |
| c |
由b2=a2-c2得
| c2 |
| a2 |
| 1 |
| 5 |
即e=
| ||
| 5 |
点评:本题主要考查圆锥曲线的综合问题,要求熟练掌握椭圆方程的求法以及直线垂直和斜率之间的关系,运算量较大.

练习册系列答案
相关题目
设实数x,y满足不等式组
,若x,y为整数,则3x+4y的最大值是( )
|
| A、26 | B、25 | C、23 | D、22 |
不等式组
的解集为( )
|
| A、{x|-2<x<-1} |
| B、{x|-1<x<0} |
| C、{x|0<x<1} |
| D、{x|x>1} |
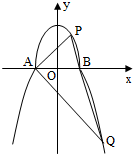 如图,曲线C由上半椭圆C1:
如图,曲线C由上半椭圆C1: