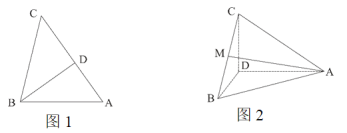
题目内容
【题目】已知椭圆![]() 的上、下焦点分别为
的上、下焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,点
,点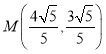 在椭圆C上,延长
在椭圆C上,延长![]() 交椭圆于N点.
交椭圆于N点.
(1)求椭圆C的方程;
(2)P,Q为椭圆上的点,记线段MN,PQ的中点分别为A,B(A,B异于原点O),且直线AB过原点O,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)最大值为3
;(2)最大值为3
【解析】
(1)利用待定系数法以及椭圆的离心率即可求解.
(2)由(1)可知![]() ,可求
,可求![]() ,与椭圆联立,设
,与椭圆联立,设![]() ,
,![]() ,根据设而不求的思想求出
,根据设而不求的思想求出![]() ,设直线
,设直线![]() ,
,
与椭圆方程联立,由弦长公式以及点到直线的距离公式求出面积表达式,借助基本不等式即可求出.
(1)依题意, ,
,
解得![]() ,
,![]() ,故椭圆C的方程为
,故椭圆C的方程为![]() ;
;
(2)由(1)可知,![]() ,故直线
,故直线![]() ,
,
设![]() ,
,![]() ,则
,则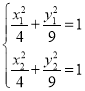 ,两式相减得
,两式相减得![]() ,
,
因为PQ不过原点,所以![]() ,即
,即![]() ,
,
同理:![]() ,
,
又因为直线AB过原点O,所以![]() ,所以
,所以![]() ,
,
设直线![]() ,
,
由 得
得![]() ,
,
由![]() ,得
,得![]() ,
,
由韦达定理得,![]() ,
,![]()
所以![]() ,
,
又因为![]() 到直线PQ的距离
到直线PQ的距离 ,
,
所以![]() ,
,
当且仅当![]() ,即
,即![]() 时等号成立,
时等号成立,
所以![]() 面积的最大值为3.
面积的最大值为3.

练习册系列答案
相关题目