题目内容
若
与
、
的夹角都是60°,而
⊥
,且|
|=|
|=|
|=1,则(
-2
)•(
+
)= .
| a |
| b |
| c |
| b |
| c |
| a |
| b |
| c |
| a |
| c |
| b |
| c |
考点:数量积表示两个向量的夹角,平面向量数量积的运算
专题:平面向量及应用
分析:
与
、
的夹角都是60°,而
⊥
,且|
|=|
|=|
|=1,可得
•
=
•
=cos60°=
,
•
=0.再利用数量积运算性质即可得出.
| a |
| b |
| c |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| 1 |
| 2 |
| b |
| c |
解答:
解:∵
与
、
的夹角都是60°,而
⊥
,且|
|=|
|=|
|=1,
∴
•
=
•
=cos60°=
,
•
=0.
∴(
-2
)•(
+
)=
•
+
•
-2
•
-2
2=
+
-0-2=-1.
故答案为:-1.
| a |
| b |
| c |
| b |
| c |
| a |
| b |
| c |
∴
| a |
| b |
| a |
| c |
| 1 |
| 2 |
| b |
| c |
∴(
| a |
| c |
| b |
| c |
| a |
| b |
| a |
| c |
| b |
| c |
| c |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:-1.
点评:本题考查了数量积的定义及其运算性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知流程图如图所示,该程序运行后,为使输出的b值为16,则循环体的判断框内①处应填( )

| A、2 | B、3 | C、4 | D、5 |
某几何体的三视图如图,若该几何体的所有顶点都在一个球面上,则该球面的表面积为( )


| A、4π | ||
B、
| ||
C、
| ||
| D、20π |
若复数z满足z(2+i)=5i-10,则|z|=( )
| A、25 | ||
B、5
| ||
C、
| ||
| D、5 |
函数f(x)=log2x-
的零点所在区间( )
| 1 |
| x |
| A、(1,2) | ||
| B、(2,3) | ||
C、(0,
| ||
D、(
|
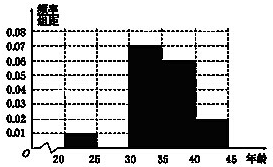 对某项活动中800名青年志愿者的年龄抽样调查后,得到如图所示的频率分布直方图,但年龄在25,30)的数据不慎丢失.依据此图,估计该项活动中年龄在25,30)的志愿者人数为
对某项活动中800名青年志愿者的年龄抽样调查后,得到如图所示的频率分布直方图,但年龄在25,30)的数据不慎丢失.依据此图,估计该项活动中年龄在25,30)的志愿者人数为