题目内容
9.在一次考试中,班主任随机抽取本班5名学生数学、物理成绩如表:| 学生序号i | 1 | 2 | 3 | 4 | 5 |
| 数学xi(分) | 89 | 91 | 93 | 95 | 97 |
| 物理yi(分) | 87 | 89 | 89 | 92 | 93 |
附:线性回归方程:$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,其中:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
分析 利用公式求出$\hat{b}$,$\hat{a}$,即可得出结论.当x=81时,带入线性回归方程预测该同学的物理成绩.
解答 解:解:样本平均数$\overline{x}$=$\frac{1}{5}(89+91+93+95+97)$=93,$\overline{y}$=$\frac{1}{5}(87+89+89+92+93)=90$,
∴$\sum _{i=1}^{6}$(xi-$\overline{x}$)(yi-$\overline{y}$)=-4×(-3)+(-2)×(-1)+0×(-1)+2×2+4×3=30
$\sum _{i=1}^{6}$ (xi-$\overline{x}$)2=16+4+0+4+16=40,
∴$\hat{b}$=$\frac{30}{40}=0.75$
∴$\hat{a}$=90-0.75×93=20.25
y关于x的线性回归方程为:$\widehat{y}$=0.75x+20.25,
当x=81时,可得y=0.75×81+20.25=81.
∴预测该同学的物理成绩为81分.
点评 本题考查线性回归方程的求法,考查最小二乘法,属于基础题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
19.函数f(x)=sin2x+$\sqrt{3}$sinxcosx的图象的一条对称轴为( )
| A. | x=$\frac{π}{12}$ | B. | x=$\frac{π}{6}$ | C. | x=$\frac{5π}{6}$ | D. | x=$\frac{7π}{12}$ |
20. 如右图是正态分布$N(μ,{σ_1}^2),N(μ,{σ_2}^2),N(μ,{σ_3}^2)({σ_1},{σ_2},{σ_3}>0)$相应的曲线,那么σ1,σ2,σ3的大小关系是( )
如右图是正态分布$N(μ,{σ_1}^2),N(μ,{σ_2}^2),N(μ,{σ_3}^2)({σ_1},{σ_2},{σ_3}>0)$相应的曲线,那么σ1,σ2,σ3的大小关系是( )
 如右图是正态分布$N(μ,{σ_1}^2),N(μ,{σ_2}^2),N(μ,{σ_3}^2)({σ_1},{σ_2},{σ_3}>0)$相应的曲线,那么σ1,σ2,σ3的大小关系是( )
如右图是正态分布$N(μ,{σ_1}^2),N(μ,{σ_2}^2),N(μ,{σ_3}^2)({σ_1},{σ_2},{σ_3}>0)$相应的曲线,那么σ1,σ2,σ3的大小关系是( )| A. | σ1>σ2>σ3 | B. | σ3>σ2>σ1 | C. | σ1>σ3>σ2 | D. | σ2>σ1>σ3 |
17.在下列四个图中,每个图的两个变量具有相关关系的图是( )


| A. | (1)(2) | B. | (1)(3) | C. | (2)(4) | D. | (2)(3) |
14.根据下表提供的数据,由散点图可知,y与x具有较好的线性相关关系,其线性回归方程为$\widehat{y}$=-0.7x+5.25,那么表中t的值为( )
| x | 1 | 2 | 3 | 4 |
| y | 4.5 | 4 | t | 2.5 |
| A. | 3 | B. | 3.15 | C. | 3.5 | D. | 4.5 |
1.sin43°cos17°+cos43°sin17°的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
18.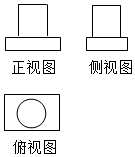 如图是某几何体的三视图,则此几何体可由下列哪两种几何体组合而成( )
如图是某几何体的三视图,则此几何体可由下列哪两种几何体组合而成( )
 如图是某几何体的三视图,则此几何体可由下列哪两种几何体组合而成( )
如图是某几何体的三视图,则此几何体可由下列哪两种几何体组合而成( )| A. | 两个长方体 | B. | 两个圆柱 | ||
| C. | 一个长方体和一个圆柱 | D. | 一个球和一个长方体 |
4.已知 f (x)=sin(x+$\frac{π}{2}$),g(x)=sin(π-x),则下列结论中正确的是( )
| A. | 函数 y=f (x)•g ( x) 的周期为 2 | |
| B. | 函数 y=f (x)•g ( x) 的最大值为 1 | |
| C. | 将f (x)的图象向左平移$\frac{π}{2}$个单位后得到 g(x)的图象 | |
| D. | y=f(x)+g(x)的一个对称中心是($\frac{3}{4}π$,0) |