Question

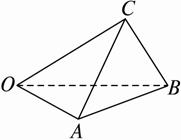
如图，三棱锥O-ABC中，OA=OB，AB=BC，∠ABC=60°．
（Ⅰ）证明：AB⊥OC；
（Ⅱ）若OA=AB=2，OC=

6

，求点O到面ABC的距离．

Answer 1

分析：（Ⅰ）取AB中点D，连接OD，CD，证明AB⊥平面OCD，可得AB⊥OC；
（Ⅱ）证明OD⊥CD，根据AB⊥OD，AB∩CD=D，可得OD⊥面ABC，从而可求点O到面ABC的距离．

解答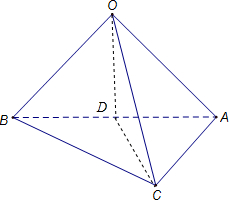：（Ⅰ）证明：取AB中点D，连接OD，CD，则
∵AB=BC，∠ABC=60°，∴BC=CA，
∵D是AB中点，
∴AB⊥CD，
∵OA=OB，D是AB中点，
∴AB⊥OD，
∵CD∩OD=D，AB⊥CD，AB⊥OD，
∴AB⊥平面OCD，
∵OC?平面OCD，
∴AB⊥OC；
（Ⅱ）∵OA=AB=2，OC=

6

，D是AB中点，
∴OD=OC=

3

，
∴OD²+CD²=OC²，
∴OD⊥CD，
∵OD⊥CD，AB⊥OD，AB∩CD=D，
∴OD⊥面ABC，
∴点O到面ABC的距离

3

．

点评：本题考查线面垂直的判定，考查点到平面的距离，正确运用线面垂直的判定是关键．