题目内容
如图，三棱锥O—ABC中，OA⊥BC，OB⊥AC，求证：OC⊥AB.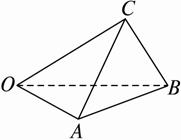
思路分析：解决这类问题首先应该找到作为基底的向量，再把相关向量表示成为基底的线性形式；充分利用本题中向量垂直关系，即他们的数量积为零，容易证明结果.
证明:令
=a、
=b、
=c为基底，
得
=b-a，
=c-a，
=c-b.
·BC=0
a·(c-b)=0
a·c=a·b.
=0
b·(c-a)=0
b·c=a·b.
得
=c·(b-a)=b·c-a·c=a·b-a·b=0，即OC⊥AB.
方法归纳 对于空间向量的研究就可以转化为对基底向量的研究，从而使问题简单化.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，三棱锥V-ABC中，VO⊥平面ABC，O∈CD，VA=VB，AD=BD，则下列结论中不一定成立的是（ ）
如图，三棱锥P-ABC的顶点P在圆柱曲线O1O上，底面△ABC内接于⊙O的直径，且∠ABC=60°，O1O=AB=4，⊙O1上一点D在平面ABC上的射影E恰为劣弧AC的中点．
如图，三棱锥O-ABC中，OA=OB，AB=BC，∠ABC=60°．
如图，三棱锥C-ABD中，AB=AD=BD=BC=CD=2，O为BD的中点，∠AOC=120°，P为AC上一点，Q为AO上一点，且