题目内容
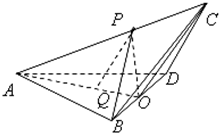 如图,三棱锥C-ABD中,AB=AD=BD=BC=CD=2,O为BD的中点,∠AOC=120°,P为AC上一点,Q为AO上一点,且
如图,三棱锥C-ABD中,AB=AD=BD=BC=CD=2,O为BD的中点,∠AOC=120°,P为AC上一点,Q为AO上一点,且| AP |
| PC |
| AQ |
| QO |
(Ⅰ)求证:PQ∥平面BCD;
(Ⅱ)求证:PO⊥平面ABD;
(Ⅲ)求BP与平面BCD所成角的正弦值.
分析:(Ⅰ)由
=
,推导出PQ∥CO,由此能推导出PQ∥平面BCD.
(Ⅱ)由等边三角形的性质和直线与平面垂直的判定定理推导出BD⊥平面AOC,再由余弦定理求出PO,然后利用勾股定理和直线与平面垂直的判定定理能证明PO⊥平面ABD.
(Ⅲ)法一:过P作PH⊥OC于H,由已知条件推导出∠PBH为BP与平面BCD所成角,由此能求出BP与平面BCD所成角的正弦值.
法二:建立空间直角坐标系,利用向量法能求出BP与平面BCD所成角的正弦值.
| AP |
| PC |
| AQ |
| QO |
(Ⅱ)由等边三角形的性质和直线与平面垂直的判定定理推导出BD⊥平面AOC,再由余弦定理求出PO,然后利用勾股定理和直线与平面垂直的判定定理能证明PO⊥平面ABD.
(Ⅲ)法一:过P作PH⊥OC于H,由已知条件推导出∠PBH为BP与平面BCD所成角,由此能求出BP与平面BCD所成角的正弦值.
法二:建立空间直角坐标系,利用向量法能求出BP与平面BCD所成角的正弦值.
解答: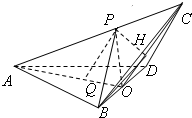 (本小题满分14分)
(本小题满分14分)
(Ⅰ)证明:∵
=
,
∴PQ∥CO…(1分)
又∵PQ不包含于平面BCD,CO?平面BCD…(2分)
∴PQ∥平面BCD…(3分)
(Ⅱ)由等边△ABD,等边△BCD,O为BD的中点得:
BD⊥AO,BD⊥OC,AO∩OC=O,
∴BD⊥平面AOC…(4分)
又∵PO?平面AOC,
∴BD⊥PO…(5分)
在△AOC中,∠AOC=120°,AO=OC=
,
∴∠OAC=30°,AC=
=3…(6分)
又∵
=2,∴AP=2,
在△APO中,由余弦定理得:PO=1…(7分)
∴PO2+AO2=AP2
∴PO⊥AO…(8分)
又AO∩BD=O,
∴PO⊥平面ABD…(9分)
(Ⅲ)方法一:过P作PH⊥OC于H,连结BH
由(Ⅱ)知BD⊥平面AOC,BD?平面BCD,
∴平面BCD⊥平面AOC,…(10分)
∴PH⊥平面BCD,
∴∠PBH为BP与平面BCD所成角 …(11分)
在Rt△CPH中,CP=1,∠PCH=30°,∠PHC=90°,
∴PH=
…(12分)
在Rt△PBO中,BO=PO=1,∠POB=90°
∴PB=
…(13分)
在Rt△PBH中,sin∠PBH=
=
=
…(14分)
∴BP与平面BCD所成角的正弦值为
.
方法二:建立如图的空间直角坐标系,
则B(1,0,0),D(-1,0,0),C(0,
,
),P(0,0,1)…(10分)
∴
=(-1,0,1),
=(1,-
,-
),
=(-2,0,0)…(11分)
设平面BCD的法向量为
=(x,y,z),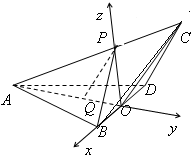
则
⇒
,
取
=(0,-
,1)…(12分)
设BP与平面BCD所成角为α,
则sinα=|cos<
,
>|=
=
…(14分)
∴BP与平面BCD所成角的正弦值为
.
 (本小题满分14分)
(本小题满分14分)(Ⅰ)证明:∵
| AP |
| PC |
| AQ |
| QO |
∴PQ∥CO…(1分)
又∵PQ不包含于平面BCD,CO?平面BCD…(2分)
∴PQ∥平面BCD…(3分)
(Ⅱ)由等边△ABD,等边△BCD,O为BD的中点得:
BD⊥AO,BD⊥OC,AO∩OC=O,
∴BD⊥平面AOC…(4分)
又∵PO?平面AOC,
∴BD⊥PO…(5分)
在△AOC中,∠AOC=120°,AO=OC=
| 3 |
∴∠OAC=30°,AC=
| OA2+OC2-2•OA•OC•cos120° |
又∵
| AP |
| PC |
在△APO中,由余弦定理得:PO=1…(7分)
∴PO2+AO2=AP2
∴PO⊥AO…(8分)
又AO∩BD=O,
∴PO⊥平面ABD…(9分)
(Ⅲ)方法一:过P作PH⊥OC于H,连结BH
由(Ⅱ)知BD⊥平面AOC,BD?平面BCD,
∴平面BCD⊥平面AOC,…(10分)
∴PH⊥平面BCD,
∴∠PBH为BP与平面BCD所成角 …(11分)
在Rt△CPH中,CP=1,∠PCH=30°,∠PHC=90°,
∴PH=
| 1 |
| 2 |
在Rt△PBO中,BO=PO=1,∠POB=90°
∴PB=
| 2 |
在Rt△PBH中,sin∠PBH=
| PH |
| PB |
| ||
|
| ||
| 4 |
∴BP与平面BCD所成角的正弦值为
| ||
| 4 |
方法二:建立如图的空间直角坐标系,
则B(1,0,0),D(-1,0,0),C(0,
| ||
| 2 |
| 3 |
| 2 |
∴
| BP |
| CB |
| ||
| 2 |
| 3 |
| 2 |
| BD |
设平面BCD的法向量为
| n |

则
|
|
取
| n |
| 3 |
设BP与平面BCD所成角为α,
则sinα=|cos<
| BP |
| n |
|
| ||||
|
|
| ||
| 4 |
∴BP与平面BCD所成角的正弦值为
| ||
| 4 |
点评:本题考查直线与平面垂直的证明,考查直线与平面所成角的正弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 如图,三棱锥V-ABC中,VA=VB=AC=BC=2,AB=
如图,三棱锥V-ABC中,VA=VB=AC=BC=2,AB= (2006•石景山区一模)如图,三棱锥P-ABC中,
(2006•石景山区一模)如图,三棱锥P-ABC中,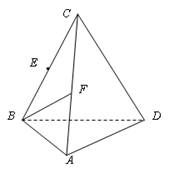
 上找一点M,在AD上找点N,使平面MED//平面BFN,说明理由;并求出
上找一点M,在AD上找点N,使平面MED//平面BFN,说明理由;并求出 的值
的值