题目内容
19.如果有穷数列a1,a2,a3,…am(m为正整数)满足a1=am,a2=am-1,…am=a1,即ai=am-i+1(i=1,2…,m),那么我们称其为对称数列.(1)设数列{bn}是项数为7的对称数列,其中b1,b2,b3,b4为等差数列,且b1=2,b4=11,依次写出数列{bn}的各项;
(2)设数列{cn}是项数为2k-1(正整数k>1)的对称数列,其中ck,ck+1,…,c2k-1是首项为50,公差为-4的等差数列.记数列{cn}的各项和为数列S2k-1,当k为何值时,S2k-1取得最大值?并求出此最大值;
(3)对于确定的正整数m>1,写出所有项数不超过2m的对称数列,使得1,2,22,…,2m-1依次为该数列中连续的项.当m>1500时,求其中一个数列的前2015项和S2015.
分析 (1)设数列{bn}的公差为d,则b4=b1+3d=2+3d=11,解得d,即可得出;
(2)利用等差数列的求和公式可求得ck+ck+1+…+c2k-1=-2k2+52k,从而可得S2k-1=2(ck+ck+1+…+c2k-1)-ck=-4(k-13)2+4×132-50,从而可得答案;
(3)依题意,可写出所有项数不超过2m的“对称数列”,依次求得每个“对称数列”前2008项的和即可.
解答 解:(1)设数列{bn}的公差为d,则b4=b1+3d=2+3d=11,解得d=3,
∴数列{bn}为2,5,8,11,8,5,2.
(2)∵ck,ck+1,…,c2k-1是首项为50,公差为-4的等差数列,
∴ck+ck+1+…+c2k-1=50k+$\frac{k(k-1)}{2}$•(-4)=-2(k2-k)+50k,
∴S2k-1=c1+c2+…+ck-1+ck+ck+1+…+c2k-1
=2(ck+ck+1+…+c2k-1)-ck
=-4(k2-k)+100k-50
=-4(k-13)2+4×132-50,
∴当k=13时,S2k-1取得最大值.S2k-1的最大值为626;
(3)所有可能的“对称数列”是:
①1,2,22,…,2m-2,2m-1,2m-2,…,22,2,1;
②1,2,22,…,2m-2,2m-1,2m-1,2m-2,…,22,2,1;
③2m-1,2m-2,…,22,2,1,2,22,…,2m-2,2m-1;
④2m-1,2m-2,…,22,2,1,1,2,22,…,2m-2,2m-1.
对于①,当m≥2015时,S2015=1+2+22+…+22014=22015-1;
当1500<m≤2014时,S2015=1+2+22+…+2m-2+2m-1+2m-2+…+22m-2016
=2m-1+2m-1-22m-2016=2m+2m-1-22m-2016-1.
对于②,当m≥2015时,S2015=22015-1.
当1500<m≤2014时,S2015=2m+1-22m-2015-1.
对于③,当m≥2015时,S2015=2m-2m-2015.
当1500<m≤2014时,S2015=2m+22016-m-3.
对于④,当m≥2015时,S2015=2m-2m-2015.
当1500<m≤2014时,S2015=2m+22015-m-2.
点评 本题考查数列的求和,突出考查等差数列的求和公式,考查抽象思维与逻辑思维、综合分析与运算能力,属于难题.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案| A. | .图象关于(π,0)中心对称 | B. | 图象关于直线$x=\frac{π}{2}$对称 | ||
| C. | 在区间$[-\frac{π}{6},0]$上单调递增 | D. | 周期为π的奇函数 |
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{7}{9}$ |
| A. | [0,$\frac{3}{2}$] | B. | [$\frac{3}{2}$,+∞) | C. | [1,$\frac{3}{2}$] | D. | [$\frac{3}{2}$,$\frac{9}{2}$] |
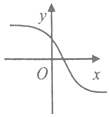
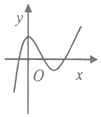
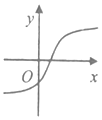
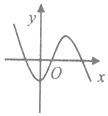
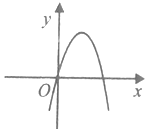 已知函数f(x)的导函数f′(x)=a(x+b)2+c(a≠0)的图象如图所示,则函数f(x)的图象可能是( )
已知函数f(x)的导函数f′(x)=a(x+b)2+c(a≠0)的图象如图所示,则函数f(x)的图象可能是( )