题目内容
已知
 恰有3个不同的零点,则实数
恰有3个不同的零点,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
A
解析试题分析:根据已知条件, ,那么可知函数的周期为1,同时结合y轴左侧的图像,数形结合法可知,要使得
,那么可知函数的周期为1,同时结合y轴左侧的图像,数形结合法可知,要使得 恰有3个不同的零点,则满足实数
恰有3个不同的零点,则满足实数 的取值范围是
的取值范围是 ,故选A.
,故选A.
考点:函数零点运用。
点评:解决分段函数的零点问题,可以采用分离为两个函数图像的交点个数来处理,数形结合思想的运用。

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
如果函数
 =x
=x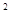 +2(a-1)x+2在区间(-∞,4)上是减函数,则实数a的取值范围是( )。
+2(a-1)x+2在区间(-∞,4)上是减函数,则实数a的取值范围是( )。
| A.a≥-3 | B. a≤-3 | C. a≤5 | D. a≥3 |
若 ,不等式
,不等式 的解集为
的解集为 ,关于
,关于 的不等式
的不等式 的解集记为
的解集记为 ,已知
,已知 是
是 的充分不必要条件,则实数
的充分不必要条件,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知 ,
, ,…
,… 为凸多边形的内角,且
为凸多边形的内角,且 ,则这个多边形是( )
,则这个多边形是( )
| A.正六边形 | B.梯形 |
| C.矩形 | D.有一个角是锐角的菱形 |
已知二次函数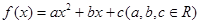 ,满足:对任意实数
,满足:对任意实数 ,都有
,都有 ,且当
,且当 时,有
时,有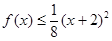 成立,又
成立,又 ,则
,则 为( )
为( )
| A.1 | B. | C.2 | D.0 |
方程 在区间
在区间 上有解,则实数
上有解,则实数 的取值范围是 ( )
的取值范围是 ( )
A. | B.  | C. | D. |
已知 则
则 的解集为( )
的解集为( )
A.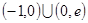 | B. |
C. | D.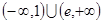 |
已知函数 ,且
,且 .则( )
.则( )
A. | B. |
C. | D. |
 的二次函数
的二次函数 的图象与端点为
的图象与端点为 、
、 的线段(包括端点)只有一个公共点,则
的线段(包括端点)只有一个公共点,则 不可能为
不可能为


