题目内容
已知函数 ,且
,且 .则( )
.则( )
A. | B. |
C. | D. |
B
解析试题分析:因为 ,所以函数
,所以函数 的对称轴为x=-1,所以函数
的对称轴为x=-1,所以函数 在(-1,+∞)单调递增,所以
在(-1,+∞)单调递增,所以 ,所以
,所以 。
。
考点:二次函数的性质。
点评:做此题的关键是根据条件 退出二次函数的对称轴。
退出二次函数的对称轴。

练习册系列答案
相关题目
已知
 恰有3个不同的零点,则实数
恰有3个不同的零点,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
.函数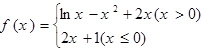 的零点的个数为( )
的零点的个数为( )
| A.0 | B.1 | C.2 | D.3 |
 ,则
,则 的大小关系是
的大小关系是
A. | B. | C. | D. |
对 ,定义
,定义 ,则函数
,则函数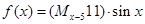 是( )
是( )
| A.奇函数但非偶函数; | B.偶函数但非奇函数; |
| C.既是奇函数又是偶函数; | D.非奇非偶函数 |
若定义在R上的偶函数 上单调递减,且
上单调递减,且 ,则不等式
,则不等式 的解集是( )
的解集是( )
A. | B. |
C. | D. |
函数f(x)=4x-3·2x+3的值域为[1,7],则f(x)的定义域为( )
| A.(-1,1)∪[2,4] ( | B.(0,1)∪[2,4] |
| C. [2,4] | D.(-∞,0] ∪[1,2] |
若 ,则
,则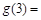 ( )
( )
A. | B. | C. | D. |
设 ,则
,则 的解集为
的解集为
A. | B. | C. | D. |