题目内容
已知二次函数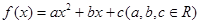 ,满足:对任意实数
,满足:对任意实数 ,都有
,都有 ,且当
,且当 时,有
时,有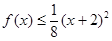 成立,又
成立,又 ,则
,则 为( )
为( )
| A.1 | B. | C.2 | D.0 |
B.
解析试题分析:由条件对任意实数x,都有f(x)≥x,知f(2)≥2成立
∵当x∈(1,3)时,有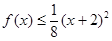 成立,
成立,
∴取x=2时, 成立,
成立,
∴f(2)=2.
∴4a+2b+c=2①
∵f(-2)=0
∴4a-2b+c=0②
由①②可得,∴4a+c=2b=1,
∴b= ,故选B.
,故选B.
考点:本题主要考查二次函数性质,方程组解法。
点评:典型题,对恒成立问题,可以任取自变量的值,式子均成立。本题紧紧围绕已知条件,通过 , f(2)=2得到方程组。
, f(2)=2得到方程组。

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
当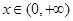 时,幂函数
时,幂函数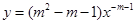 为减函数,则实数
为减函数,则实数 ( )
( )
| A.m=2 | B.m=-1 | C.m=2或m=-1 | D. |
按复利计算,存入一笔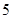 万元的三年定期存款,年利率为
万元的三年定期存款,年利率为 ,则
,则 年后支取可获得利息为( )
年后支取可获得利息为( )
A. 万元 万元 | B. 万元 万元 |
C. 万元 万元 | D. 万元 万元 |
已知 的单调递增区间为
的单调递增区间为 ,则实数a的取值范围是
,则实数a的取值范围是
A. | B.(1,4) | C.(2,4) | D. |
设函数 ,则满足
,则满足 的
的 的值是( )
的值是( )
| A.2 | B.16 | C.2或16 | D.-2或16 |
已知
 恰有3个不同的零点,则实数
恰有3个不同的零点,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
函数f(x)= (a>0,a≠1)的图象恒过定点( ).
(a>0,a≠1)的图象恒过定点( ).
A. | B. | C. | D. |
二次函数 的图象的对称轴为
的图象的对称轴为 ,则当
,则当 时,
时, 的值为( )
的值为( )
A. | B.1 | C.17 | D.25 |
对 ,定义
,定义 ,则函数
,则函数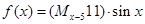 是( )
是( )
| A.奇函数但非偶函数; | B.偶函数但非奇函数; |
| C.既是奇函数又是偶函数; | D.非奇非偶函数 |