题目内容
(本小题满分12分)
四棱锥S-ABCD中,侧面SAD是正三角形,底面ABCD是正方形,且平面SAD⊥平面ABCD,M、N分别是AB、SC的中点.
(Ⅰ)求证:MN∥平面SAD;
(Ⅱ)求二面角S-CM-D的余弦值.
(Ⅰ)证明略,(Ⅱ)
【解析】
试题分析:要证明线面平行先寻求线线平行,由于M、N分别是AB、SC的中点,取 的中点
的中点 ,连接
,连接
,然后证明四边形 是平行四边形即可,第二步求二面角可用空间向量法,首先取
是平行四边形即可,第二步求二面角可用空间向量法,首先取 、
、 的中点
的中点 、
、 ,连结OS,过
,连结OS,过 作AD的垂线交BC于G,分别以OA,OG,OS为x,y,z轴,建立坐标系,写出相关点的坐标,由于平面
作AD的垂线交BC于G,分别以OA,OG,OS为x,y,z轴,建立坐标系,写出相关点的坐标,由于平面 的法向量为
的法向量为 ,本题只需求平面
,本题只需求平面 的法向量,最后利用二面角公式 借助法向量坐标求出二面角的余弦值.
的法向量,最后利用二面角公式 借助法向量坐标求出二面角的余弦值.
试题解析:(Ⅰ)如图,取 的中点
的中点 ,连结
,连结 ,
,

则 ,且
,且 ,
, ,所以
,所以 ,且
,且 ,所以四边形
,所以四边形 是平行四边形,则
是平行四边形,则 ,由于
,由于 平面
平面 ,
,
 平面
平面 外,所以
外,所以 平面
平面 .
.
(Ⅱ)取 的中点
的中点 ,连结
,连结 ,过
,过 作
作 的垂线交
的垂线交 于
于 ,分别以
,分别以 ,
, ,
, 为
为 轴,建立坐标系,
轴,建立坐标系, ,
, ,
, ,
, ,
, ,
,

设面 的法向量为
的法向量为 ,
,
则 有
有
令 ,
, ,取面ABCD的法向量
,取面ABCD的法向量 ,
,
则 ,
,
所以二面角 的余弦值为
的余弦值为 .
.
[解法二]:如图,取 的中点
的中点 ,连结
,连结 、
、 ,连结SH,由
,连结SH,由 ,且面
,且面 ⊥面
⊥面 ,所以
,所以 平面
平面 ,易得
,易得 ,所以
,所以 ,则
,则 ,所以
,所以 ,则有
,则有 ,所以
,所以 是二面角
是二面角 的平面角,
的平面角,
设 ,则
,则 ,
, ,
, ,
, ,
, ,
,
则
 ,所以二面角
,所以二面角 的余弦值为
的余弦值为 .
.
考点:1.线面平行判定定理;2.二面角的求法;

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 有最大值
有最大值 ,求实数
,求实数 的值.
的值.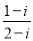 对应的点位于( )
对应的点位于( ) ,若将其图象向右平移
,若将其图象向右平移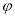 (
(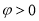 )个单位后所得的图象关于原点对称,则
)个单位后所得的图象关于原点对称,则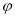 的最小值为( )
的最小值为( )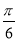 B.
B.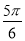 C.
C.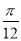 D.
D.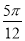
 的共轭复数对应的点位于( )
的共轭复数对应的点位于( )
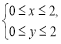 所表示的平面区域内任取一点P,若点P的坐标(x,y)满足
所表示的平面区域内任取一点P,若点P的坐标(x,y)满足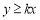 的概率为
的概率为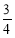 ,则实数k=( )
,则实数k=( )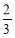 (D)
(D)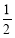
 满足
满足 ,则
,则 的最小值为 .
的最小值为 . 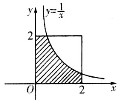
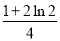 B.
B. 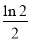
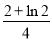 D.
D.