题目内容
16．如图，直线l是曲线y=f（x）在x=4处的切线，则f′（4）=$\frac{1}{2}$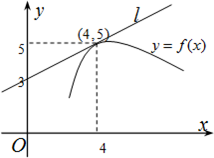
分析 运用两点的斜率公式，可得直线l的斜率，再由导数的几何意义：函数在某点处的导数即为曲线在该点处的切线的斜率，即可得到所求值．
解答 解：由图象可得直线l经过点（0，3）和切点（4，5），
则直线l的斜率为k=$\frac{5-3}{4-0}$=$\frac{1}{2}$，
由导数的几何意义，可得f′（4）=k=$\frac{1}{2}$．
故答案为：$\frac{1}{2}$．
点评 本题考查导数的几何意义：函数在某点处的导数即为曲线在该点处的切线的斜率，同时考查两点的斜率公式，考查运算能力，属于基础题．
练习册系列答案
阳光同学一线名师全优好卷系列答案
相关题目
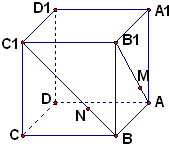在正方体ABCD-A1B1C1D1中，点M、N分别在AB1，BC1上，且AM=$\frac{1}{3}$AB1，BN=$\frac{1}{3}$BC1，则下列结论：
6．二项式（a-1）8的展开式中，最大的二项式系数为（ ）
| A． | C${\;}_{8}^{4}$ | B． | -C${\;}_{8}^{4}$ | C． | C${\;}_{9}^{5}$ | D． | -C${\;}_{9}^{5}$ |