题目内容
7.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一个焦点恰为抛物线y2=8x的焦点,且离心率为2,则该双曲线的标准方程为( )| A. | ${x^2}-\frac{y^2}{3}=1$ | B. | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | C. | $\frac{x^2}{3}-{y^2}=1$ | D. | $\frac{x^2}{12}-\frac{y^2}{4}=1$ |
分析 求得抛物线的焦点(2,0),可得c=2,运用离心率公式可得a=1,再由a,b,c的关系,解得b,进而得到双曲线的方程.
解答 解:抛物线y2=8x的焦点为(2,0),
由题意得$e=\frac{c}{a}=\frac{2}{a}=2$,解得a=1,
又b2=c2-a2=4-1=3.
故双曲线的标准方程为${x^2}-\frac{y^2}{3}=1$.
故选:A.
点评 本题考查双曲线的方程的求法,注意运用抛物线的焦点和离心率公式,以及双曲线的基本量的关系,考查运算能力,属于基础题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
15.过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}={1^{\;}}({a>b>0})$右焦点作双曲线其中一条渐近线的垂线与两渐近线分别交于A,B两点,O为坐标原点,且△AOB的面积为$\frac{{6{a^2}}}{5}$,则该双曲线的离心率为( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{5}}}{3}$ | C. | $\frac{{\sqrt{13}}}{2}$ | D. | $\frac{{\sqrt{13}}}{3}$ |
12.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线的斜率为k,k是mn的最小值,其中m,n满足$\frac{1}{m}+\frac{1}{n}=\sqrt{mn}$,且右焦点与抛物线y2=4$\sqrt{5}$x的焦点重合,则该双曲线的离心率等于( )
| A. | $\sqrt{2}$ | B. | 2$\sqrt{5}$ | C. | 2 | D. | $\sqrt{5}$ |
17.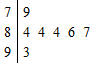 我校为了丰富同学们的课余生活,特举办了一次挑战主持人大赛,如图是七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
我校为了丰富同学们的课余生活,特举办了一次挑战主持人大赛,如图是七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
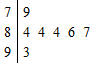 我校为了丰富同学们的课余生活,特举办了一次挑战主持人大赛,如图是七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
我校为了丰富同学们的课余生活,特举办了一次挑战主持人大赛,如图是七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )| A. | 4;4 | B. | 5;1.6 | C. | 84;4 | D. | 85;1.6 |
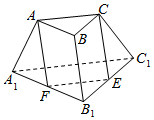 在三棱台ABC-A1B1C1中,A1B1=2AB,点E、F分别是棱B1C1、A1B1的中点,则在三棱台的各棱所在的直线中,与平面ACEF平行的有A1C1、BB1.
在三棱台ABC-A1B1C1中,A1B1=2AB,点E、F分别是棱B1C1、A1B1的中点,则在三棱台的各棱所在的直线中,与平面ACEF平行的有A1C1、BB1.