题目内容
设f(x)为奇函数,且当x>0时,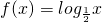
(Ⅰ)求当x<0时,f(x)的解析表达式;
(Ⅱ)解不等式f(x)≤2.
解:(Ⅰ)设x<0时,
则 .
.
所以:当x<0时,f(x)=-log (-x).
(-x).
(Ⅱ)由题意,得 .
.
所以不等式f(x)≤2的解集为:{x|x≥ 或-4≤x<0}
或-4≤x<0}
分析:(Ⅰ)直接设设x<0,则-x>0,代入所给解析式,再结合f(x)为奇函数即可求出结论;
(Ⅱ)直接根据分段函数的特点分段求解,再合并即可.
点评:本题主要考查函数奇偶性的应用以及不等式的解法.考查函数的基本性质,解决此类问题需要对函数奇偶性的性质掌握比较熟练.
则
 .
.所以:当x<0时,f(x)=-log
 (-x).
(-x).(Ⅱ)由题意,得
 .
.所以不等式f(x)≤2的解集为:{x|x≥
 或-4≤x<0}
或-4≤x<0}分析:(Ⅰ)直接设设x<0,则-x>0,代入所给解析式,再结合f(x)为奇函数即可求出结论;
(Ⅱ)直接根据分段函数的特点分段求解,再合并即可.
点评:本题主要考查函数奇偶性的应用以及不等式的解法.考查函数的基本性质,解决此类问题需要对函数奇偶性的性质掌握比较熟练.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
设f(x)为奇函数,且在(-∞,0)内是减函数,f(-2)=0,则xf(x)<0的解集为( )
| A、(-1,0)∪(2,+∞) | B、(-∞,-2)∪(0,2) | C、(-∞,-2)∪(2,+∞) | D、(-2,0)∪(0,2 |