题目内容
(2014·孝感模拟)已知函数f(x)=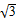
sinωxcosωx-cos2ωx,其中ω为使f(x)能在x=
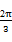时取得最大值的最小正整数.
(1)求ω的值.
(2)设△ABC的三边长a,b,c满足b2=ac,且边b所对的角θ的取值集合为M,当x∈M时,求f(x)的值域.
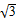sinωxcosωx-cos2ωx,其中ω为使f(x)能在x=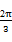时取得最大值的最小正整数.(1)求ω的值.
(2)设△ABC的三边长a,b,c满足b2=ac,且边b所对的角θ的取值集合为M,当x∈M时,求f(x)的值域.
（1）2 （2）
.
.(1)f(x)=sin
-
,依题意有
-
=2kπ+
(k∈Z),
即ω=
(k∈Z),ω的最小正整数值为2,所以ω=2.
(2)b2=ac,又b2=a2+c2-2accosB,
所以a2+c2-2accosB=ac,即1+2cosB=
≥
=2,
所以1+2cosB≥2,所以cosB≥,所以0<B≤
,
即M=
,
f(x)=sin
-,0<x≤,
所以-<4x-≤
,
所以sin∈
,
所以f(x)∈,
故函数f(x)的值域是.
-,依题意有-=2kπ+(k∈Z),即ω=
(k∈Z),ω的最小正整数值为2,所以ω=2.(2)b2=ac,又b2=a2+c2-2accosB,
所以a2+c2-2accosB=ac,即1+2cosB=
≥=2,所以1+2cosB≥2,所以cosB≥
,所以0<B≤,即M=
,f(x)=sin
-,0<x≤,所以-
<4x-≤,所以sin
∈,所以f(x)∈
,故函数f(x)的值域是
.
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
的图象沿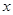
轴向左平移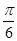
个单位后，得到一个关于
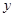轴对称的图象，则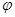
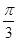
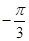
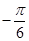
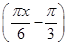(0≤x≤9)的最大值与最小值之和为( )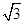
．
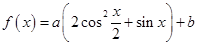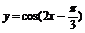的单调减区间是 . 
cosωx,x∈R,又f(α)=-2,f(β)=0,且|α-β|的最小值为
,则正数ω的值为( )
满足下了列哪些条件（填序号）__________．
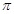为最小周期；
上单调递增；
成中心对称．
在区间[0，
]上的最大值是________．
，函数
在
上单调递减．则
的取值范围是 （ ）
