题目内容
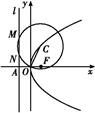
在平面直角坐标系xOy中,抛物线C的顶点在原点,经过点A(2,2),其焦点F在x轴上.
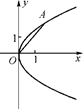
(1)求抛物线C的标准方程;
(2)求过点F,且与直线OA垂直的直线的方程;
(3)设过点M(m,0)(m>0)的直线交抛物线C于D、E两点,ME=2DM,记D和E两点间的距离为f(m),求f(m)关于m的表达式.

(1)求抛物线C的标准方程;
(2)求过点F,且与直线OA垂直的直线的方程;
(3)设过点M(m,0)(m>0)的直线交抛物线C于D、E两点,ME=2DM,记D和E两点间的距离为f(m),求f(m)关于m的表达式.
(1)y2=2x(2)x+y- =0(3)
=0(3) (m>0)
(m>0)
 =0(3)
=0(3) (m>0)
(m>0)(1)由题意,可设抛物线C的标准方程为y2=2px.因为点A(2,2)在抛物线C上,所以p=1.因此抛物线C的标准方程为y2=2x.
(2)由(1)可得焦点F的坐标是 ,又直线OA的斜率为
,又直线OA的斜率为 =1,故与直线OA垂直的直线的斜率为-1,因此所求直线的方程是x+y-
=1,故与直线OA垂直的直线的斜率为-1,因此所求直线的方程是x+y- =0.
=0.

(3)(解法1)设点D和E的坐标分别为(x1,y1)和(x2,y2),直线DE的方程是y=k(x-m),k≠0.
将x= +m代入y2=2x,有ky2-2y-2km=0,解得y1,2=
+m代入y2=2x,有ky2-2y-2km=0,解得y1,2= .
.
由ME=2DM知1+ =2(
=2( -1),化简得k2=
-1),化简得k2= .
.
因此DE2=(x1-x2)2+(y1-y2)2= (y1-y2)2=
(y1-y2)2= (m2+4m),所以f(m)=
(m2+4m),所以f(m)= (m>0).
(m>0).
(解法2)设D ,E
,E .
.
由点M(m,0)及 =2
=2 ,得
,得 t2-m=2
t2-m=2 ,t-0=2(0-s).因此t=-2s,m=s2.所以f(m)=DE=
,t-0=2(0-s).因此t=-2s,m=s2.所以f(m)=DE= (m>0).
(m>0).
(2)由(1)可得焦点F的坐标是
 ,又直线OA的斜率为
,又直线OA的斜率为 =1,故与直线OA垂直的直线的斜率为-1,因此所求直线的方程是x+y-
=1,故与直线OA垂直的直线的斜率为-1,因此所求直线的方程是x+y- =0.
=0.
(3)(解法1)设点D和E的坐标分别为(x1,y1)和(x2,y2),直线DE的方程是y=k(x-m),k≠0.
将x=
 +m代入y2=2x,有ky2-2y-2km=0,解得y1,2=
+m代入y2=2x,有ky2-2y-2km=0,解得y1,2= .
.由ME=2DM知1+
 =2(
=2( -1),化简得k2=
-1),化简得k2= .
.因此DE2=(x1-x2)2+(y1-y2)2=
 (y1-y2)2=
(y1-y2)2= (m2+4m),所以f(m)=
(m2+4m),所以f(m)= (m>0).
(m>0).(解法2)设D
 ,E
,E .
.由点M(m,0)及
 =2
=2 ,得
,得 t2-m=2
t2-m=2 ,t-0=2(0-s).因此t=-2s,m=s2.所以f(m)=DE=
,t-0=2(0-s).因此t=-2s,m=s2.所以f(m)=DE= (m>0).
(m>0).
练习册系列答案
相关题目
 上的任意一点
上的任意一点 到该抛物线焦点的距离比该点到
到该抛物线焦点的距离比该点到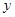 轴的距离多1.
轴的距离多1.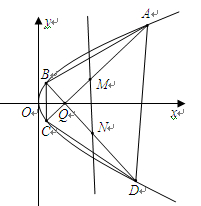
 的值;
的值;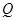 (2,0)且互相垂直的两条直线
(2,0)且互相垂直的两条直线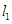 、
、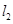 分别与该抛物线分别交于
分别与该抛物线分别交于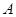 、
、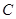 、
、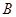 、
、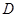 四点.
四点.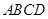 面积的最小值;
面积的最小值;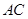 、
、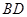 的中点分别为
的中点分别为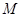 、
、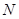 两点,试问:直线
两点,试问:直线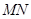 是否过定点?若是,求出定点坐标;若不是,请说明理由.
是否过定点?若是,求出定点坐标;若不是,请说明理由.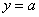 交抛物线
交抛物线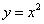 于
于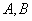 两点.若该抛物线上存在点
两点.若该抛物线上存在点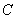 ,使得
,使得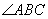 为直角,则
为直角,则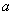 的取值范围为________.
的取值范围为________. 为抛物线
为抛物线 的焦点,
的焦点, 为该抛物线上三点,若
为该抛物线上三点,若 ,则
,则 ( )
( )