题目内容
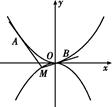
已知抛物线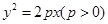 上的任意一点
上的任意一点 到该抛物线焦点的距离比该点到
到该抛物线焦点的距离比该点到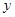 轴的距离多1.
轴的距离多1.
(1)求 的值;
的值;
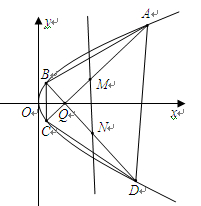
(2)如图所示,过定点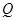 (2,0)且互相垂直的两条直线
(2,0)且互相垂直的两条直线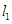 、
、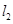 分别与该抛物线分别交于
分别与该抛物线分别交于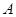 、
、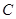 、
、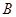 、
、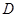 四点.
四点.
(i)求四边形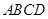 面积的最小值;
面积的最小值;
(ii)设线段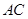 、
、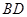 的中点分别为
的中点分别为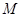 、
、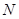 两点,试问:直线
两点,试问:直线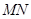 是否过定点?若是,求出定点坐标;若不是,请说明理由.
是否过定点?若是,求出定点坐标;若不是,请说明理由.
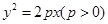 上的任意一点
上的任意一点 到该抛物线焦点的距离比该点到
到该抛物线焦点的距离比该点到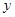 轴的距离多1.
轴的距离多1.
(1)求
 的值;
的值;(2)如图所示,过定点
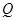 (2,0)且互相垂直的两条直线
(2,0)且互相垂直的两条直线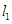 、
、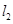 分别与该抛物线分别交于
分别与该抛物线分别交于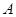 、
、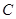 、
、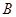 、
、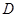 四点.
四点.(i)求四边形
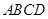 面积的最小值;
面积的最小值;(ii)设线段
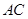 、
、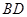 的中点分别为
的中点分别为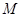 、
、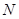 两点,试问:直线
两点,试问:直线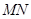 是否过定点?若是,求出定点坐标;若不是,请说明理由.
是否过定点?若是,求出定点坐标;若不是,请说明理由.(1)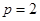 (2)(i)四边形
(2)(i)四边形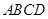 面积的最小值是48(ii)
面积的最小值是48(ii)
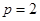 (2)(i)四边形
(2)(i)四边形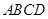 面积的最小值是48(ii)
面积的最小值是48(ii)试题分析:(1)直接利用抛物线的定义
(2)(i)
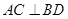 S四边形ABCD,
S四边形ABCD,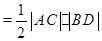 ,利用弦长
,利用弦长公式,以及基本不等式,二次函数在闭区间上的最值问题
的解法求解
(ii)恒过定点问题的常规解法
试题解析:
(1)由已知
 ∴
∴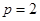
(2)(i)由题意可设直线
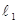 的方程为
的方程为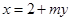 (
(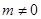 ),代入
),代入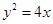 得
得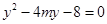
设
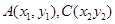 则
则 ,
,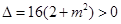
∴
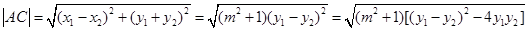
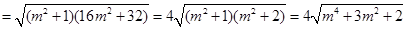 6分
6分同理可得
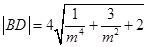 7分
7分S四边形ABCD
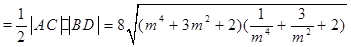
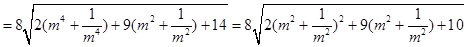 8分
8分设
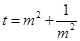 则
则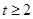 ∴S四边形ABCD
∴S四边形ABCD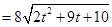
∵函数
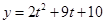 在
在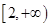 上是增函数
上是增函数∴S四边形ABCD
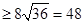 ,当且仅当即
,当且仅当即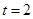 即
即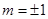 时取等号
时取等号∴四边形
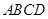 面积的最小值是48. 9分
面积的最小值是48. 9分(ii)由①得
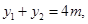 ∴
∴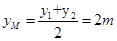 ∴
∴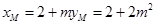
∴
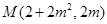 , 11分
, 11分同理得
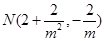 12分
12分∴直线的方程可表示为
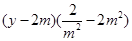
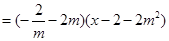
即
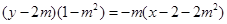
当
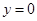 时得
时得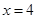
∴直线
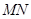 过定点(4,0). 14分
过定点(4,0). 14分注:第(2)中的第(i)问:
S四边形ABCD
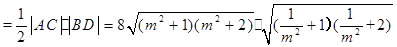
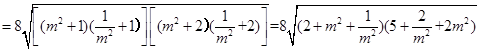
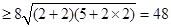 (当且仅当
(当且仅当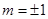 时取等号)也可.
时取等号)也可.
练习册系列答案
相关题目
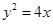 .
.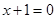 相切,求所有的圆都经过的定点坐标;
相切,求所有的圆都经过的定点坐标;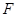 ,若过
,若过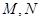 两点,若
两点,若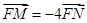 ,求直线
,求直线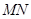 的斜率;
的斜率;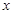 正半轴上
正半轴上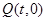 点的直线与该抛物线交于
点的直线与该抛物线交于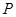 为抛物线上异于
为抛物线上异于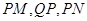 连线的斜率为
连线的斜率为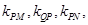 试求满足
试求满足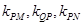 成等差数列的充要条件.
成等差数列的充要条件.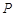 与定点
与定点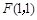 和直线
和直线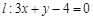 的距离相等,则动点
的距离相等,则动点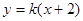 (k>0)与抛物线
(k>0)与抛物线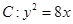 相交于
相交于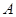 、
、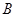 两点,
两点,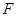 为
为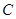 的焦点,若
的焦点,若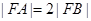 ,则k的值为( )
,则k的值为( )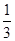
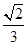
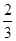
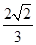
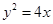 上一点
上一点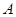 的横坐标为
的横坐标为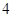 ,则点
,则点 (k>0)与抛物线
(k>0)与抛物线 相交于A、B两点,
相交于A、B两点, 为
为 的焦点,若
的焦点,若 ,则k的值为
,则k的值为



 时,拱顶离水面2米,水面宽4米,水位下降1米后,水面宽 米.
时,拱顶离水面2米,水面宽4米,水位下降1米后,水面宽 米.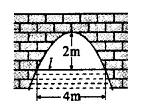
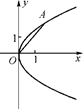
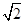 时,切线MA的斜率为-
时,切线MA的斜率为-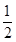 .
.