题目内容
已知向量
=(2cosx,-cos(x+
)),
=(cosx,2sin(x+
)),记f(x)=
•
.
(Ⅰ)求函数f(x)的最小正周期和单调递减区间;
(Ⅱ)在△ABC中,角A,B,C的对边分别为a,b,c,若f(
)=1,a=2,b=
,求sinC的值.
| m |
| π |
| 12 |
| n |
| π |
| 12 |
| m |
| n |
(Ⅰ)求函数f(x)的最小正周期和单调递减区间;
(Ⅱ)在△ABC中,角A,B,C的对边分别为a,b,c,若f(
| A |
| 2 |
| 3 |
考点:余弦定理,平面向量数量积的运算,三角函数中的恒等变换应用
专题:三角函数的图像与性质,解三角形
分析:(Ⅰ)由三角函数中的恒等变换应用可得函数解析式为f(x)=1-sin(2x+
),可求T,由-
+2kπ≤2x+
≤
+2kπ,k∈Z,可解得单调递减区间.
(Ⅱ)由f(
)=1-sin(A+
)=1,可解得A,cosA,由正弦定理可得sinB,cosB,从而可求sinC=sin(A+B)的值.
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
(Ⅱ)由f(
| A |
| 2 |
| π |
| 6 |
解答:
解:(Ⅰ)∵f(x)=
•
=2cos2x-2sin(x+
)cos(x+
)=1-sin(2x+
),
∴T=
=π,
∴由-
+2kπ≤2x+
≤
+2kπ,k∈Z,可解得:x∈[kπ-
,kπ+
],k∈Z,
∴单调递减区间为:[kπ-
,kπ+
],k∈Z.
(Ⅱ)∵f(
)=1-sin(A+
)=1,可解得:A+
=kπ,k∈Z,
∴由A为三角形内角,可得A=
,cosA=-
.
∴由正弦定理可得:sinB=
=
=
,cosB=
=
,
∴sinC=sin[π-(A+B)]=sin(A+B)=sinAcosB+cosAsinB=
×
-
×
=
.
| m |
| n |
| π |
| 12 |
| π |
| 12 |
| π |
| 6 |
∴T=
| 2π |
| 2 |
∴由-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
∴单调递减区间为:[kπ-
| π |
| 3 |
| π |
| 6 |
(Ⅱ)∵f(
| A |
| 2 |
| π |
| 6 |
| π |
| 6 |
∴由A为三角形内角,可得A=
| 5π |
| 6 |
| ||
| 2 |
∴由正弦定理可得:sinB=
| bsinA |
| a |
| ||||
| 2 |
| ||
| 4 |
| 1-sin2B |
| ||
| 4 |
∴sinC=sin[π-(A+B)]=sin(A+B)=sinAcosB+cosAsinB=
| 1 |
| 2 |
| ||
| 4 |
| ||
| 2 |
| ||
| 4 |
| ||
| 8 |
点评:本题主要考查了平面向量数量积的运算,三角函数中的恒等变换应用,正弦函数的图象和性质,属于基础题.

练习册系列答案
相关题目
点A是抛物线C1:y2=2px(p>0)与双曲线C2:
-
=1(a>0,b>0)的一条渐近线的交点(异于原点),若点A到抛物线C1的准线的距离为p,则双曲线C2的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
执行以下程序框图,所得的结果为( )
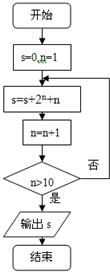

| A、1067 | B、2100 |
| C、2101 | D、4160 |
方程ln(2x+1)=
的一个根落在区间( )(参考数值:ln1.5≈0.41,ln2≈0.69,ln2.5≈0.92)
| 1 |
| 3x+2 |
A、(-
| ||||
B、(0,
| ||||
C、(
| ||||
D、(
|
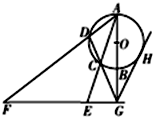 如图所示,AB是⊙O的直径,G为AB延长线上的一点,GCD是⊙O的割线,过点G作 AB的垂线,交AC的延长线于点 E,交AD的延长线于点F,过G作⊙O的切线,切点为H,求证:
如图所示,AB是⊙O的直径,G为AB延长线上的一点,GCD是⊙O的割线,过点G作 AB的垂线,交AC的延长线于点 E,交AD的延长线于点F,过G作⊙O的切线,切点为H,求证: 如图,已知圆O:x2+y2=64分别与x轴、y轴的正半轴交于点A、B,直线l:y=kx-k+2分别于x轴、y轴的正半轴交于点N、M.
如图,已知圆O:x2+y2=64分别与x轴、y轴的正半轴交于点A、B,直线l:y=kx-k+2分别于x轴、y轴的正半轴交于点N、M.