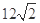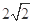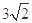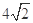题目内容
已知圆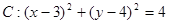 和直线
和直线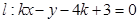
(1) 求证:不论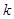 取什么值,直线和圆总相交;
取什么值,直线和圆总相交;
(2) 求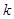 取何值时,圆被直线截得的弦最短,并求最短弦的长.
取何值时,圆被直线截得的弦最短,并求最短弦的长.
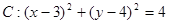 和直线
和直线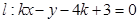
(1) 求证:不论
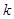 取什么值,直线和圆总相交;
取什么值,直线和圆总相交;(2) 求
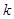 取何值时,圆被直线截得的弦最短,并求最短弦的长.
取何值时,圆被直线截得的弦最短,并求最短弦的长. (1)见解析 (2) 当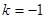 时,圆被直线截得最短的弦长为4
时,圆被直线截得最短的弦长为4
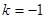 时,圆被直线截得最短的弦长为4
时,圆被直线截得最短的弦长为4(1)由直线l的方程可得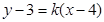 从而可确定直线l恒过定点(4,3),
从而可确定直线l恒过定点(4,3),
再证明定点(4,3)在圆内部即可.
(2)由弦长公式可知当定点P(4,3)为弦的中点时,圆心到直线l的距离最大,弦长最短,所以此时直线l与CP垂直.
解:(1)证明:由直线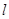 的方程可得,
的方程可得,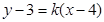 ,则直线
,则直线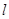 恒通过点
恒通过点
 ,把
,把 代入圆C的方程,得
代入圆C的方程,得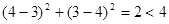 ,所以点
,所以点 在圆的内部,
在圆的内部,
又因为直线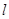 恒过点
恒过点 , 所以直线
, 所以直线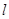 与圆C总相交.
与圆C总相交.
(2)设圆心到直线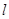 的距离为
的距离为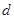 ,则
,则
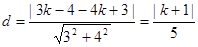
又设弦长为 ,则
,则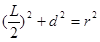 ,即
,即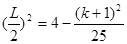 .
.
∴当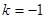 时,
时, 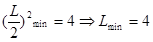
所以圆被直线截得最短的弦长为4.
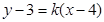 从而可确定直线l恒过定点(4,3),
从而可确定直线l恒过定点(4,3),再证明定点(4,3)在圆内部即可.
(2)由弦长公式可知当定点P(4,3)为弦的中点时,圆心到直线l的距离最大,弦长最短,所以此时直线l与CP垂直.
解:(1)证明:由直线
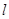 的方程可得,
的方程可得,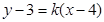 ,则直线
,则直线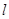 恒通过点
恒通过点 ,把
,把 代入圆C的方程,得
代入圆C的方程,得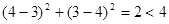 ,所以点
,所以点 在圆的内部,
在圆的内部,又因为直线
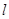 恒过点
恒过点 , 所以直线
, 所以直线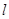 与圆C总相交.
与圆C总相交.(2)设圆心到直线
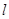 的距离为
的距离为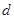 ,则
,则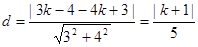
又设弦长为
 ,则
,则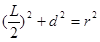 ,即
,即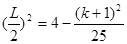 .
.∴当
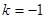 时,
时, 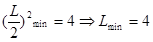
所以圆被直线截得最短的弦长为4.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
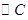 与两平行直线
与两平行直线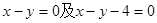 都相切,且圆心
都相切,且圆心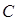 在直线
在直线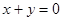 上,
上,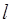 与
与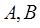 两点,
两点,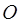 为坐标原点且满足
为坐标原点且满足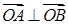 ,求直线
,求直线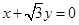 绕原点按顺时针方向旋转
绕原点按顺时针方向旋转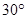 所得直线与圆
所得直线与圆 的位置关系是( ).
的位置关系是( ).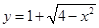 与直线
与直线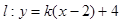 有两个不同的交点,实数
有两个不同的交点,实数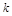 的范围是()
的范围是()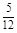 ,+∞)
,+∞)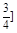
 ,
,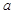 为任意实数时,直线
为任意实数时,直线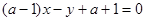 恒过定点
恒过定点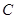 ,则以
,则以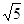 为半径的圆的方程是_____________.
为半径的圆的方程是_____________.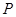 是直线
是直线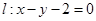 上的动点,点
上的动点,点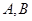 分别是圆
分别是圆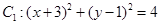 和圆
和圆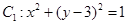 上的两个动点,则
上的两个动点,则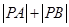 的最小值为
的最小值为  中,圆
中,圆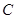 的方程为
的方程为 ,若直线
,若直线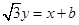 上至少存在一点,使得以该点为圆心,1为半径的圆与圆
上至少存在一点,使得以该点为圆心,1为半径的圆与圆 的最大值是 ;
的最大值是 ; 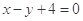 被圆
被圆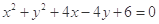 截得的弦长等于( )
截得的弦长等于( )