��Ŀ����
20�����������ĸ����⣺�����⡰?x��R��x2��0���ķ��ǡ�?x��R��x2��0����
�ں���y=f��x���Ķ�����Ϊ��-�ޣ�-1���ȣ�1��+�ޣ�����ͼ������һ��P��x��y������x2-y2=1������y=f��x���������溯����
����a��b��[0��1]����ʽa2+b2��$\frac{1}{4}$�����ĸ�����$\frac{��}{4}$
�ܺ���y=log2��x2-ax+2����[2��+�ޣ���Ϊ������ ʵ��a��ȡֵ��Χ�ǣ�-�ޣ�$\frac{5}{2}$����
���������������Ǣ٢ڢܣ����������������������ţ�
���� �ٸ��ݺ������ʵ�����ķ����жϣ�
�ڸ��ݺ�����ż�ԵĶ�������ʽ��˫���ߵ�ͼ������жϣ�
�۸��ݼ��θ��͵ĸ��ʹ�ʽ�����жϣ�
�����ò���ʽ����������ò������뷨��������жϼ��ɣ�
��� 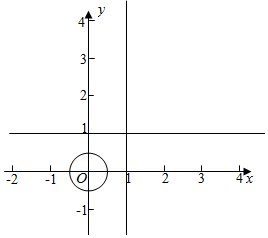 �⣺�����⡰?x��R��x2��0���ķ��ǡ�?x��R��x2��0�����ʢ���ȷ��
�⣺�����⡰?x��R��x2��0���ķ��ǡ�?x��R��x2��0�����ʢ���ȷ��
�ں���y=f��x���Ķ�����Ϊ��-�ޣ�-1���ȣ�1��+�ޣ�����ͼ������һ��P��x��y������x2-y2=1������y=f��x���������溯������ȷ������P����������y=$\left\{\begin{array}{l}{\sqrt{{x}^{2}-1}}&{x��-1}\\{-\sqrt{{x}^{2}-1}}&{x��1}\end{array}\right.$ʱ������f��x��Ϊ�溯�����ʢ���ȷ��
����a��b��[0��1]����ʽ${a^2}+{b^2}��\frac{1}{4}$�����ĸ�����$P=\frac{{\frac{1}{4}���С�{{��{\frac{1}{2}}��}^2}}}{1��1}=\frac{��}{16}$����ͼ�����Ԣ۴���
����Ϊ����y=log2��x2-ax+2����[2��+�ޣ��Ϻ�Ϊ����
������[2��+�ޣ���x2-ax+2��1�������
������[2��+�ޣ���$a��x+\frac{1}{x}$�������
��$g��x��=x+\frac{1}{x}$��$g�䣨x��=1-\frac{1}{{x}^{2}}$
��Ϊx��2������$g�䣨x��=1-\frac{1}{{x}^{2}}��0$��
����g��x����[2��+�ޣ���Ϊ��������
���ԣ���x=2ʱ��g��x������СֵΪg��2��=$\frac{5}{2}$��
����$a��\frac{5}{2}$����ʵ��a��ȡֵ��Χ�ǣ�-�ޣ�$\frac{5}{2}$�����ʢ���ȷ��
�ʴ�Ϊ���٢ڢ�
���� ���⿼��������������жϣ���ȷ�������֪ʶ����������Ҫ����������Ӧ�ã�

| A�� | 252 | B�� | -252 | C�� | 160 | D�� | -160 |
| A�� | ��СֵΪ-1�����������ֵ | B�� | ��СֵΪ2�����������ֵ | ||
| C�� | ���ֵΪ-1����������Сֵ | D�� | ���ֵΪ2����������Сֵ |
| A�� | $\frac{5}{2}$ | B�� | 2 | C�� | $\frac{\sqrt{10}}{4}$ | D�� | $\frac{\sqrt{10}}{2}$ |
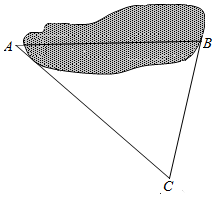 A��B����֮�����һ��ˮ������ͼ������ѡ����һ��C�����CA=10$\sqrt{7}$km��CB=10km����CBA=60�㣮
A��B����֮�����һ��ˮ������ͼ������ѡ����һ��C�����CA=10$\sqrt{7}$km��CB=10km����CBA=60�㣮