题目内容
已知函数
(Ⅰ)若 试确定函数
试确定函数 的单调区间;
的单调区间;
(Ⅱ)若 ,且对于任意
,且对于任意 ,
, 恒成立,求实数
恒成立,求实数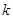 的取值范围;
的取值范围;
(Ⅲ)令 若至少存在一个实数
若至少存在一个实数 ,使
,使 成立,求实数
成立,求实数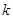 的取值范围.
的取值范围.

(Ⅰ)若
 试确定函数
试确定函数 的单调区间;
的单调区间;(Ⅱ)若
 ,且对于任意
,且对于任意 ,
, 恒成立,求实数
恒成立,求实数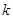 的取值范围;
的取值范围;(Ⅲ)令
 若至少存在一个实数
若至少存在一个实数 ,使
,使 成立,求实数
成立,求实数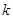 的取值范围.
的取值范围.(Ⅰ)单调递增区间是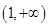 ,单调递减区间是
,单调递减区间是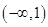 ;(Ⅱ)
;(Ⅱ)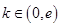 ;(Ⅲ)
;(Ⅲ)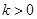 .
.
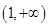 ,单调递减区间是
,单调递减区间是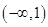 ;(Ⅱ)
;(Ⅱ)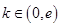 ;(Ⅲ)
;(Ⅲ)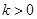 .
.试题分析:(Ⅰ)求出函数的导数,令导数大于零解得单调增区间,令导数小于零得单调减区间;(Ⅱ)令导数等于零得
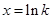 ,然后对
,然后对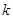 在
在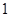 处断开进行讨论,在
处断开进行讨论,在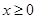 上求出函数的最小值,令其大于零解得
上求出函数的最小值,令其大于零解得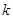 的范围;(Ⅲ)由于存在
的范围;(Ⅲ)由于存在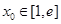 ,使
,使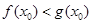 ,则
,则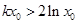
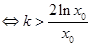 ,令
,令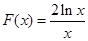 ,则
,则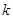 大于
大于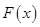 的最小值.
的最小值.试题解析:(Ⅰ)由
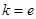 得
得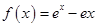 ,所以
,所以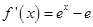 .
. 由
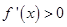 得
得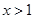 ,故
,故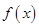 的单调递增区间是
的单调递增区间是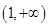 , 3分
, 3分由
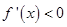 得
得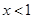 ,故
,故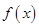 的单调递减区间是
的单调递减区间是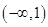 . 4分
. 4分(Ⅱ) 由
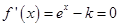 得
得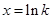 . 5分
. 5分 ①当
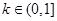 时,
时,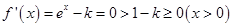 .此时
.此时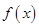 在
在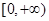 上单调递增.故
上单调递增.故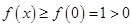 ,符合题意. 6分
,符合题意. 6分②当
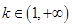 时,
时,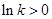 .当
.当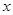 变化时
变化时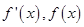 的变化情况如下表:
的变化情况如下表: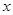 | 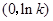 | 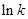 | 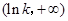 |
 | 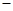 |  | 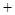 |
 | 单调递减 | 极小值 | 单调递增 |
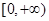 上,
上,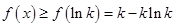 . 8分
. 8分依题意,
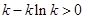 ,又
,又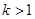 ,所以
,所以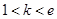 .
.综合①,②得,实数
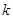 的取值范围是
的取值范围是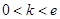 . 9分
. 9分(Ⅲ)由于存在
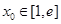 ,使
,使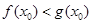 ,则
,则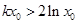
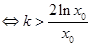
令
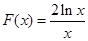 ,则
,则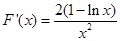 12分
12分当
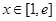 时,
时,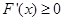 (仅当
(仅当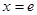 时取等号)
时取等号)
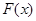 在
在 上单调递增,
上单调递增,
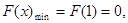 因此
因此 . 14分
. 14分
练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
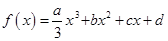 (其中
(其中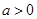 ),且方程
),且方程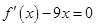 的两个根分别为
的两个根分别为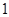 、
、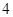 .
.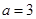 且曲线
且曲线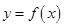 过原点时,求
过原点时,求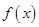 的解析式;
的解析式;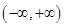 无极值点,求
无极值点,求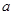 的取值范围.
的取值范围. .
. 时,求函数
时,求函数 的极值;
的极值; ,使函数
,使函数 在
在 上有唯一的零点,若有,请求出
上有唯一的零点,若有,请求出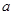 的范围;若没有,请说明理由.
的范围;若没有,请说明理由.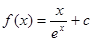
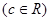
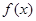 的单调区间、最大值;
的单调区间、最大值;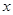 的方程
的方程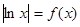 的根的个数.
的根的个数.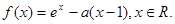
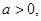 求函数
求函数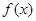 在
在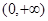 上的极值;
上的极值;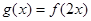 ,设函数
,设函数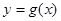 的图像
的图像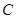 与
与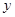 轴交于
轴交于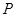 点,曲线
点,曲线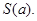 则当
则当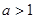 时,求
时,求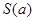 的最小值.
的最小值.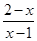 +aln(x-1)(a∈R).
+aln(x-1)(a∈R).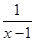 <2ln(x-1)<2x-4(x>2);
<2ln(x-1)<2x-4(x>2);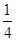 +
+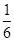 +…+
+…+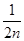 <lnn<1+
<lnn<1+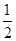 + +
+ +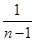 (n∈N*,且n≥2).
(n∈N*,且n≥2).
 ,给出定义:
,给出定义: 是函数
是函数 的导函数,
的导函数, 是
是 有实数解
有实数解 ,则称点
,则称点 为函数
为函数 的“拐点”。某同学经研究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且拐点就是对称中心。若
的“拐点”。某同学经研究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且拐点就是对称中心。若 ,请你根据这一发现,求:(1)函数
,请你根据这一发现,求:(1)函数 =________.
=________. 所表示的平面区域为D,直线
所表示的平面区域为D,直线 与D有公共点,则
与D有公共点,则 的取值范围是________
的取值范围是________ ,其导函数记为
,其导函数记为 ,则
,则
 .
.