题目内容
2.命题p:实数x满足a<x<3a,其中a>0;q:实数x满足2<x≤3.(Ⅰ)若a=1,且p∧q为真,求实数x的取值范围;
(Ⅱ)若q是p的充分条件,求实数a的取值范围.
分析 (I)当a=1时,命题p:实数x满足1<x<3;q:实数x满足2<x≤3.p∧q为真,可得$\left\{\begin{array}{l}{1<x<3}\\{2<x≤3}\end{array}\right.$,解得x范围.
(II)由于q是p的充分条件,可得$\left\{\begin{array}{l}{a≤2}\\{3<3a}\\{a>0}\end{array}\right.$,解出即可.
解答 解:(I)当a=1时,命题p:实数x满足1<x<3;q:实数x满足2<x≤3.
∵p∧q为真,∴$\left\{\begin{array}{l}{1<x<3}\\{2<x≤3}\end{array}\right.$,解得2<x<3.
∴实数x的取值范围为(2,3).
(II)∵q是p的充分条件,∴$\left\{\begin{array}{l}{a≤2}\\{3<3a}\\{a>0}\end{array}\right.$,
解得1<a≤2.
∴实数a的取值范围是(1,2].
点评 本题考查了简易逻辑的判定方法、不等式的解法、集合的运算,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.设集合A={x|x2-x-2<0},B={x|-1<x<1},则( )
| A. | A?B | B. | B⊆A | C. | A=B | D. | A∩B=∅ |
7.如果实数x,y满足条件$\left\{\begin{array}{l}{x-2y+2≥0}\\{2x-y-2≤0}\\{x+y-1≥0}\end{array}\right.$,則z=3x-2y的最小值为( )
| A. | -4 | B. | -2 | C. | 1 | D. | 2 |
14.下列函数是偶函数的是( )
| A. | y=x3 | B. | y=2x2-3 | C. | y=x | D. | y=x2,x∈[0,1] |
11.集合A={1,3},B={1,2,3,4},则A∩B=( )
| A. | {1,2} | B. | {1,4} | C. | {1} | D. | {1,3} |




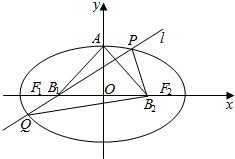 如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1、F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为1的直角三角形.
如图,设椭圆的中心为原点O,长轴在x轴上,上顶点为A,左、右焦点分别为F1、F2,线段OF1,OF2的中点分别为B1,B2,且△AB1B2是面积为1的直角三角形.