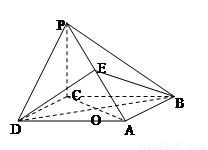题目内容
如图,四棱锥 的底面
的底面 是矩形,
是矩形, ,
, ,且侧面PAB是正三角形,平面
,且侧面PAB是正三角形,平面 平面ABCD,E是棱PA的中点。
平面ABCD,E是棱PA的中点。
 的底面
的底面 是矩形,
是矩形, ,
, ,且侧面PAB是正三角形,平面
,且侧面PAB是正三角形,平面 平面ABCD,E是棱PA的中点。
平面ABCD,E是棱PA的中点。
(1)求证: 平面EBD;
平面EBD;
(2)求三棱锥 的体积。
的体积。
 平面EBD;
平面EBD;(2)求三棱锥
 的体积。
的体积。解:(1)证明:在矩形ABCD 中,连结AC ,设AC 、BD 交点为O ,则O是AC中点
又E是PA中点,所以EO是△PAC 的中位线,
所以PC//EO
又EO 平面EBD ,PC
平面EBD ,PC 平面EBD
平面EBD
所以PC// 平面EBD
(2) 取AB中点H,则由PA=PB ,得PH ⊥AB ,
又平面PAB ⊥平面ABCD ,且平面PAB ∩平面ABCD=AB ,
所以PH ⊥平面ABCD
取AH 中点F ,由E 是PA 中点,得EF//PH ,
所以EF⊥平面ABCD
∵ ,
,
由题意可求得: =
= ,PH=
,PH= ,EF=
,EF= ,
,
 。
。

又E是PA中点,所以EO是△PAC 的中位线,
所以PC//EO
又EO
 平面EBD ,PC
平面EBD ,PC 平面EBD
平面EBD所以PC// 平面EBD
(2) 取AB中点H,则由PA=PB ,得PH ⊥AB ,
又平面PAB ⊥平面ABCD ,且平面PAB ∩平面ABCD=AB ,
所以PH ⊥平面ABCD
取AH 中点F ,由E 是PA 中点,得EF//PH ,
所以EF⊥平面ABCD
∵
 ,
,由题意可求得:
 =
= ,PH=
,PH= ,EF=
,EF= ,
,  。
。

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目

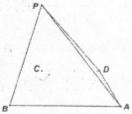
 的底面是平行四边形,
的底面是平行四边形, 平面
平面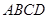 ,
,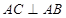 ,
,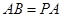 ,
,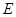 是
是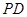 上的点,且
上的点,且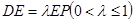 .
.
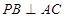 ;
;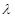 的值,使
的值,使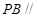 平面
平面 ;
;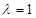 时,求三棱锥
时,求三棱锥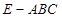 与四棱锥
与四棱锥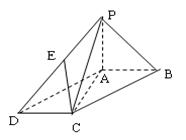
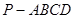 的底面
的底面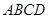 是正方形,侧棱
是正方形,侧棱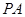
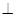 底面
底面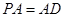 ,
,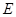 、
、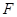 分别是棱
分别是棱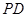 、
、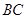 的中点.
的中点. 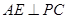 ; (2) 求直线
; (2) 求直线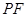 与平面
与平面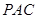 所成的角的正切值
所成的角的正切值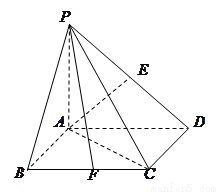
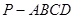 的底面是边长为
的底面是边长为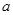 的菱形,
的菱形,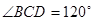 ,
,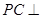 平面
平面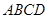 ,
,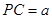 ,
,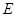 为
为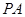 的中点,O为底面对角线的交点;
的中点,O为底面对角线的交点;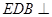 平面
平面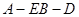 的正切值。
的正切值。