题目内容
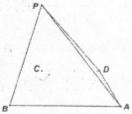
（09年山东实验中学诊断三理）（13分）如图：四棱锥
的底面
是提醒，腰
，
平分
且与
垂直，侧面
都垂直于底面，平面
与底面成60°角
（1）求证：
；
（2）求二面角
的大小
解析：
（1）证明：因为 侧面
都垂直于底面
，
所以 
面
所以 
又因为
所以 
面
所以
（2）解：因为 在等腰梯形中，对角
与
互补
又因为
平分
且与
垂直，
所以
所以
过点
作
，垂足为点
， 连结
则
便是平面
与底面所成二面角的平面角
即
， 在
中， 求得：
所以在
中，求得：
如图建立空间直角坐标系
，
所以
设平面的法向量为
=（
）
则
所以
；
设平面
的法向量为
，
则
所以
所以 二面角
的大小为
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
（注：
）
（1）若函数
在
上为增函数，求正实数
的取值范围；
时，若直线
与函数
的图象在
上有两个不同交点，求实数
的取值范围：
的上、下焦点分别为
，点
为坐标平面的动点，满足
（1）求动点
的方方程；
作曲线
，求直线
的方程；
上是否存在点
，过该点的坐标：若不存在。试说明理由
，已知它们的图像在
处有相同的切线，
和
的解析式
在区间
上是单调减函数，求实数
的取值范围。
中，
的值
，求