题目内容

19．已知a，b，c∈R+，且a+b+c=1，是否存在实数k，使得不等式$\sqrt{4a+1}$+$\sqrt{4b+1}$+$\sqrt{4c+1}$＜k恒成立？如果存在，试求出k的取值范围；如果不存在，请说明理由．

分析 由题意可得（$\sqrt{4a+1}$+$\sqrt{4b+1}$+$\sqrt{4c+1}$）max＜k，运用柯西不等式，可得最大值，即可得到k的范围．

解答 解：由柯西不等式可得
（1•$\sqrt{4a+1}$+1•$\sqrt{4b+1}$+1•$\sqrt{4c+1}$）2≤（12+12+12）（4a+1+4b+1+4c+1）
=3×（4+3）=21．
当且仅当4a+1=4b+1=4c+1，即a=b=c=$\frac{1}{3}$时，取得等号．
即有$\sqrt{4a+1}$+$\sqrt{4b+1}$+$\sqrt{4c+1}$的最大值为$\sqrt{21}$．
故存在实数k，使得不等式$\sqrt{4a+1}$+$\sqrt{4b+1}$+$\sqrt{4c+1}$＜k恒成立．
则k的取值范围是（$\sqrt{21}$，+∞）．

点评 本题考查不等式恒成立问题的解法，考查柯西不等式的运用：求最值，属于中档题．

练习册系列答案
相关题目
9．设函数f（x）的定义域为R，有下列四个命题：
①若存在常数M，使得对任意的x∈R，有f（x）≤M，则M是函数f（x）的最大值；
②若存在x0∈R，使得对任意的x∈R，且x≠x0，有f（x）＜f（x0），则f（x0）是函数f（x）的最大值；
③若存在x0∈R，使得对任意的x∈R，有f（x）＜f（x0），则f（x0）是函数f（x）的最大值；
④若存在x0∈R，使得对任意的x∈R，有f（x）≤f（x0），则f（x0）是函数f（x）的最大值；
这些命题中，正确命题的个数是（　　）
A．0B．1C．2D．3
10．已知函数f（x）=x+$\frac{2}{x}$（x＞0）．
（1）点P为该函数图象上任意一点，求点P到直线：y=-x-1的距离的最小值；
（2）过点（$\sqrt{2}$，3）作直线l与该函数的图象交于A，B两个不同的点，且A，B关于直线y=-$\sqrt{2}$x+m对称，求m的值．
7．不等式|x-3|＞2的解集是{x|x＜1，或x＞5 }．
14．已知函数f（x）=2x，g（x）=（2-lnx）•lnx+b（b∈R），记h（x）=f（x）-$\frac{1}{f（x）}$
（1）若h（x0）=$\frac{8}{3}$，求实数x0的值
（2）若存在x1，x2∈[1，+∞），使得h（x1）=g（x2），求实数b的取值范围
（3）若g（x）＜0，对于x∈（0，+∞）恒成立，试问是否存在实数x，使得h[g（x）]=-b成立，若存在，求出实数x的值，若不存在，说明理由．
4．线段|AB|=4，|PA|+|PB|=6，M是AB中点，当点P在同一平面运动时，PM长度的最大值3．
11．已知函数f（x）=$\frac{xlnx}{x+1}$和直线l：y=m（x-1）．
（1）当曲线y=f（x）在点（1，f（1））处的切线与直线l垂直时，求原点O到直线l的距离；
（2）若对于任意的x∈[1，+∞），f（x）≤m（x-1）恒成立，求m的取值范围．
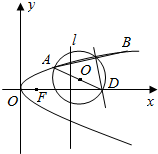8．如图，抛物线y2=2px（p＞0），F为抛物线的焦点，A，B是抛物线上互异的两点，直线AB与x轴不垂直，线段AB的中垂线交x轴于D（a，0），m=|$\overrightarrow{AF}$|+|$\overrightarrow{BF}$|．
（1）证明：a是p，m的等差中项；
（2）若m=3p，l为平行于y轴的直线，且l被以AD为直径的动圆所截得的弦长恒为定值，求直线l的方程．
9．已知非空集合A⊆N，且满足条件“若x∈A则（10-x）∈A“，试写出满足条件且只含有2个元素的所有集合A．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网