Question

8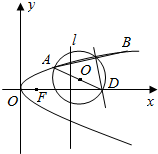．如图，抛物线y²=2px（p＞0），F为抛物线的焦点，A，B是抛物线上互异的两点，直线AB与x轴不垂直，线段AB的中垂线交x轴于D（a，0），m=|$\overrightarrow{AF}$|+|$\overrightarrow{BF}$|．
（1）证明：a是p，m的等差中项；
（2）若m=3p，l为平行于y轴的直线，且l被以AD为直径的动圆所截得的弦长恒为定值，求直线l的方程．

Answer 1

分析 （1）由条件，抛物线的准线方程为j：x=-$\frac{p}{2}$，F（0，$\frac{p}{2}$），设线段AB的中点为C，过A作AP⊥j于P，过B作BQ⊥j于Q，过C作CR⊥j于R，设A，B的坐标，可得C的坐标，证明2a=m+p，即可证明a是p，m的等差中项；
（2）求出l被以AD为直径的动圆所截得的弦长，利用l被以AD为直径的动圆所截得的弦长恒为定值，即可求直线l的方程．

解答 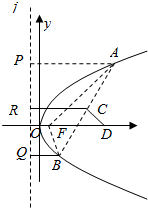（1）证明：由条件，抛物线的准线方程为j：x=-$\frac{p}{2}$，F（$\frac{p}{2}$，0），设线段AB的中点为C，过A作AP⊥j于P，过B作BQ⊥j于Q，过C作CR⊥j于R，
设A（2pt_A²，2pt_A），B（2pt_B²，2pt_B），则C（p（t_A²+t_B²），p（t_A+t_B）），
∵CR=p（t_A²+t_B²）+$\frac{p}{2}$，
∴m+p=|AF|+|BF|+p=|AP|+|BQ|+p=2CR+p=2p（t_A²+t_B²+1），
∵k_AB=$\frac{2p{t}_{B}-2p{t}_{A}}{2p{{t}_{B}}^{2}-2p{{t}_{A}}^{2}}$=$\frac{1}{{t}_{A}+{t}_{B}}$，
∴k_CD=-（t_A+t_B），
∴直线CD：y=-（t_A+t_B）[x-p（t_A²+t_B²）]+p（t_A+t_B），
∴a=p（t_A²+t_B²）+p
∴2a=m+p，
∴a是p，m的等差中项；
（2）解：由（1）m=3p时，D（2p，0），令A（2pt_A²，2pt_A），
则以AD为直径的圆E，E的坐标为（p（t_A²+1），pt_A），半径r=p$\sqrt{{{t}_{A}}^{4}-{{t}_{A}}^{2}+1}$，
设直线l：x=k，作EG⊥l于G，则EG=|p（t_A²+1）-k|，
∴l被以AD为直径的动圆所截得的弦长2$\sqrt{{t}^{2}-E{G}^{2}}$=2$\sqrt{p（2k-3p）{{t}_{A}}^{2}+2pk-{k}^{2}}$，
∵为定值，
∴2k-3p=0，
∴k=$\frac{3p}{2}$，
∴直线l：x=$\frac{3p}{2}$．

点评 本题考查抛物线的方程于性质，考查等差中项的证明，考查直线与圆的位置关系，综合性强．