题目内容
设函数 ,
, .
.
(1)记 为
为 的导函数,若不等式
的导函数,若不等式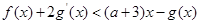 在
在 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;
(2)若 ,对任意的
,对任意的 ,不等式
,不等式 恒成立.求
恒成立.求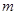 (
(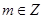 ,
, )的值.
)的值.
 ,
, .
.(1)记
 为
为 的导函数,若不等式
的导函数,若不等式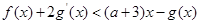 在
在 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;(2)若
 ,对任意的
,对任意的 ,不等式
,不等式 恒成立.求
恒成立.求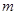 (
(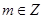 ,
, )的值.
)的值.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)先利用不等式整理得
 ,所以
,所以 ,设
,设 ,用求导的方法求出
,用求导的方法求出 ;(2)设出函数
;(2)设出函数 ,由题意可判断
,由题意可判断 在
在 递增,所以
递增,所以 恒成立,转化为
恒成立,转化为 恒成立,下面只需求
恒成立,下面只需求 .
.试题解析:(1)不等式
 ,即为
,即为 ,
,化简得:
 ,
,由
 知
知 ,因而
,因而 ,设
,设 ,
,由

∵当
 时
时 ,
, ,∴
,∴ 在
在 时成立.
时成立.由不等式有解,可得知
 ,即实数
,即实数 的取值范围是
的取值范围是 6分
6分(2)当
 ,
, .
.由
 恒成立,得
恒成立,得 恒成立,
恒成立,设
 .
.由题意知
 ,故当
,故当 时函数
时函数 单调递增,
单调递增,∴
 恒成立,即
恒成立,即 恒成立,
恒成立,因此,记
 ,得
,得 ,
,∵函数在
 上单调递增,在
上单调递增,在 上单调递减,
上单调递减,∴函数
 在
在 时取得极大值,并且这个极大值就是函数
时取得极大值,并且这个极大值就是函数 的最大值.由此可得
的最大值.由此可得 ,故
,故 ,结合已知条件
,结合已知条件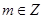 ,
, ,可得
,可得 . 12分
. 12分
练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
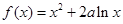 .
.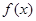 的图象在
的图象在 处的切线斜率为
处的切线斜率为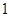 ,求实数
,求实数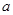 的值;
的值;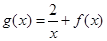 在
在 上是减函数,求实数
上是减函数,求实数 -
-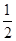 alnx,a∈R.
alnx,a∈R.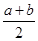 )≤
)≤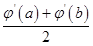 ≤φ′(
≤φ′(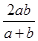 ).
).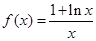 .
.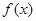 在区间
在区间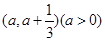 上存在极值点,求实数
上存在极值点,求实数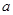 的取值范围;
的取值范围;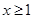 时,不等式
时,不等式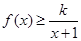 恒成立,求实数
恒成立,求实数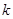 的取值范围;
的取值范围;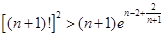 .(
.(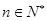 ,
,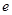 为自然对数的底数)
为自然对数的底数) .
.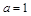 时,求函数
时,求函数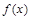 的单调增区间;
的单调增区间;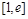 上的最小值.
上的最小值.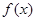
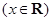 满足
满足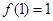 ,
,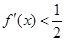 ,则不等式
,则不等式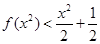 的解集为______.
的解集为______.
 ,且当
,且当
 满足
满足





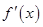 是函数
是函数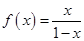 的导数,则
的导数,则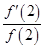 的值是( )
的值是( )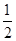
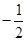
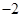
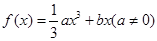 ,若f(3)="3f" ′(x0),则x0=( )
,若f(3)="3f" ′(x0),则x0=( )