题目内容
19．不等式2x3-3x2+x＞0的解集为（0，$\frac{1}{2}$）∪（1，+∞）．分析 2x3-3x2+x＞0分解因式可得x（2x-1）（x-1）＞0，解得0＜x＜$\frac{1}{2}$，或x＞1，即可得到不等式的解集．
解答 解：2x3-3x2+x＞0分解因式可得x（2x-1）（x-1）＞0，
解得0＜x＜$\frac{1}{2}$，或x＞1，
故不等式的解集为（0，$\frac{1}{2}$）∪（1，+∞），
故答案为：（0，$\frac{1}{2}$）∪（1，+∞）．
点评 本题考查高次不等式的解法，分解因式是解决问题的关键，属基础题．
练习册系列答案
名校课堂系列答案
相关题目
如图，在平行四边形ABB1A1中，AB=4，AA1=2，∠ABB1=60°，C，C1分别是AB，A1B1的中点，现把平行四边形AA1C1C沿C1C折起到A′A′1C1C，连接B1C，B1A′，B1A′1，BA′．
10．设A={1，2，（m2-3m+1）+（m2-5m-6）i}，B={-1，5}，A∩B={5}，则实数m的值为（ ）
| A． | -1 | B． | -4 | C． | -1或4 | D． | 1或-4 |
14．设m≠n，x=m4-m3n，y=mn3-n4，则x，y的大小关系是（ ）
| A． | x＞y | B． | x=y | C． | x＜y | D． | 与m，n的取值有关 |
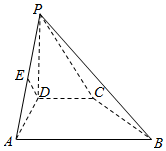如图，在四棱锥P-ABCD中，PD⊥面ABCD，AB∥DC，AB⊥AD，DC=6，AD=8，BC=10，∠PAD=45°，E为PA的中点．