题目内容
定义在R上的函数f(x)满足f(x)=
,则f(2014)的值为 .
|
考点:分段函数的应用
专题:计算题,函数的性质及应用
分析:由于x>0时,f(x)=f(x-1),即有f(x+1)=f(x),推得f(2014+x)=f(x),则f(2014)=f(0),再由分段函数表达式,即可求出答案.
解答:
解:x>0时,f(x)=f(x-1),
即有f(x+1)=f(x),推得f(2014+x)=f(x)
则f(2014)=f(0)=log216=4,
故答案为:4.
即有f(x+1)=f(x),推得f(2014+x)=f(x)
则f(2014)=f(0)=log216=4,
故答案为:4.
点评:本题考查分段函数及运用,考查函数的性质及运用,考查基本的对数运算能力,属于基础题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
已知数列的前四项为1×2,2×3,3×4,4×5,则下列可以做为该数列通项的是( )
| A、2n |
| B、n+1 |
| C、n2+n |
| D、n2-n |
| E、n2+n |
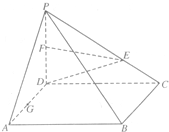 如图,ABCD是正方形,PD⊥底面ABCD,点E在PC上,F,G分别是PD和AD的中点.
如图,ABCD是正方形,PD⊥底面ABCD,点E在PC上,F,G分别是PD和AD的中点.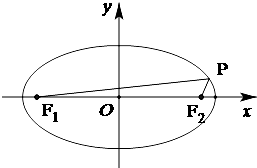 已知椭圆
已知椭圆