题目内容
已知定义在R上的函数 满足
满足 ,当
,当 时,
时, ,且
,且 .
.
(1)求 的值;
的值;
(2)当 时,关于
时,关于 的方程
的方程 有解,求
有解,求 的取值范围.
的取值范围.
(1)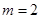 ,
,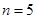 (2)
(2)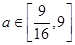
解析试题分析:(1)由 可知
可知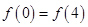 ,代入表达式可求得
,代入表达式可求得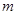 的值.又
的值.又 ,可求出
,可求出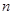 的值;(2)由(1)可知方程为
的值;(2)由(1)可知方程为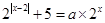 ,对x进行讨论去绝对值符号,可得
,对x进行讨论去绝对值符号,可得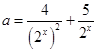 ,
,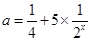 据
据 结合指数函数,二次函数的性质可求得
结合指数函数,二次函数的性质可求得 的取值范围.
的取值范围.
试题解析:解:(1)由已知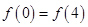 ,可得
,可得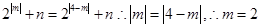
又由 可知
可知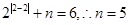 . 5分
. 5分
(2)方程即为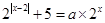 在
在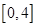 有解.
有解.
当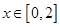 时,
时,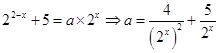 ,令
,令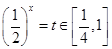 ,
,
则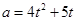 在
在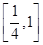 单增,
单增,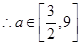
当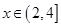 时,
时,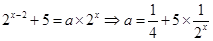 ,令
,令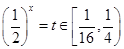 ,
,
则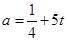 ,
,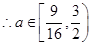 ,
,
综上: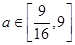 . 14分
. 14分
考点:本题主要考查指数函数,二次函数求值域和分类讨论的数学思想方法.

练习册系列答案
相关题目
 为偶函数.
为偶函数. 的值;
的值; 有且只有一个根,求实数
有且只有一个根,求实数 的取值范围.
的取值范围.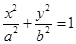 (a>b>0)的离心率为
(a>b>0)的离心率为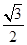 ,过其右焦点F与长轴垂直的弦长为1,
,过其右焦点F与长轴垂直的弦长为1, (万元)可以看成月产量
(万元)可以看成月产量 (吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元. 为偶函数.
为偶函数. 的解析式;
的解析式;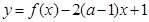 在区间(2,3)上为单调函数,求实数
在区间(2,3)上为单调函数,求实数 的取值范围.
的取值范围. .
. ,
, ,
, ,证明:
,证明: 在区间
在区间 内存在唯一的零点;
内存在唯一的零点; ,若对任意
,若对任意 、
、 ,有
,有 ,求
,求 的取值范围.
的取值范围.
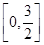 上的最大值.
上的最大值.