题目内容
已知数列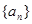 中,
中,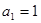 ,
, ,数列
,数列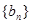 中,
中,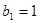 ,且点
,且点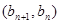 在直线
在直线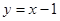 上。
上。
(1)求数列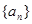 的通项公式;
的通项公式;
(2)求数列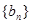 的前
的前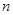 项和
项和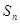 ;
;
(3)若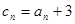 ,求数列
,求数列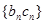 的前
的前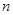 项和
项和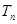 ;
;
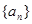 中,
中,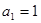 ,
, ,数列
,数列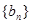 中,
中,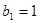 ,且点
,且点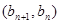 在直线
在直线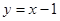 上。
上。(1)求数列
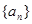 的通项公式;
的通项公式;(2)求数列
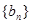 的前
的前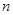 项和
项和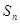 ;
;(3)若
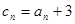 ,求数列
,求数列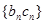 的前
的前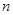 项和
项和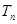 ;
;(1) (2)
(2) 
(3)
 (2)
(2) 
(3)

第一问中利用数列的递推关系式
 ,因此得到数列
,因此得到数列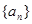 的通项公式;
的通项公式;
第二问中,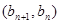 在
在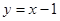 即为:
即为:
即数列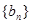 是以
是以 的等差数列
的等差数列
得到其前n项和。
第三问中,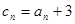 又
又 

 ,利用错位相减法得到。
,利用错位相减法得到。
解:(1)
 即数列
即数列 是以
是以 为首项,2为公比的等比数列
为首项,2为公比的等比数列

 ……4分
……4分
(2)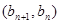 在
在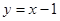 即为:
即为:
即数列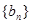 是以
是以 的等差数列
的等差数列

 ……8分
……8分
(3)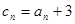 又
又 


 ①
①  ②
②
①- ②得到



 ,因此得到数列
,因此得到数列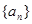 的通项公式;
的通项公式;第二问中,
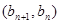 在
在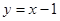 即为:
即为:
即数列
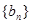 是以
是以 的等差数列
的等差数列得到其前n项和。
第三问中,
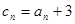 又
又 

 ,利用错位相减法得到。
,利用错位相减法得到。解:(1)

 即数列
即数列 是以
是以 为首项,2为公比的等比数列
为首项,2为公比的等比数列
 ……4分
……4分(2)
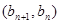 在
在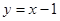 即为:
即为:
即数列
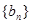 是以
是以 的等差数列
的等差数列
 ……8分
……8分(3)
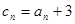 又
又 


 ①
①  ②
②①- ②得到



练习册系列答案
相关题目
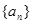 的前项和为
的前项和为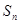 ,已知
,已知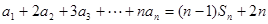 (
(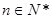 ).
).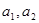 的值;
的值;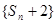 是等比数列;
是等比数列;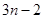 项,……,余下的项顺序不变,组成一个新数列
项,……,余下的项顺序不变,组成一个新数列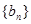 ,若
,若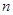 项的和为
项的和为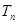 ,求证:
,求证: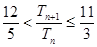 .
.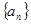 满足
满足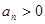 且对一切
且对一切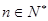 ,
,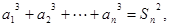
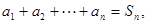
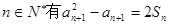
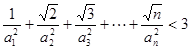
 的前
的前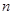 项和为
项和为 ,且
,且 (
( N*),其中
N*),其中 .
. (
( N*).
N*). ;
; .
.
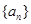 为等差数列,且
为等差数列,且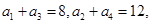 (Ⅰ)求数列
(Ⅰ)求数列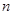 项和为
项和为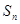 ,若
,若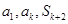 成等比数列,求正整数
成等比数列,求正整数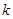 的值。
的值。 是公差不为零的等差数列,
是公差不为零的等差数列, ,且
,且 、
、 、
、 成等比数列。
成等比数列。 ,求数列
,求数列 的前
的前 项和
项和 。
。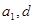 为实数,首项为
为实数,首项为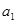 ,公差为
,公差为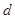 的等差数列
的等差数列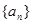 的前n项和为
的前n项和为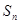 ,满足
,满足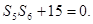
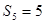 ,求
,求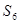 及
及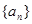 满足
满足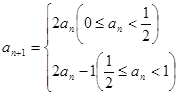 若
若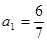 ,则
,则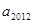 的值为:( )
的值为:( )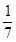
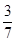
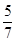
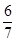
 的前20项之和
的前20项之和 ,则
,则 =( )
=( )