题目内容
已知数列 的前
的前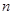 项和为
项和为 ,且
,且 (
( N*),其中
N*),其中 .
.
(Ⅰ) 求 的通项公式;
的通项公式;
(Ⅱ) 设 (
( N*).
N*).
①证明: ;
;
② 求证: .
.
 的前
的前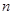 项和为
项和为 ,且
,且 (
( N*),其中
N*),其中 .
.(Ⅰ) 求
 的通项公式;
的通项公式;(Ⅱ) 设
 (
( N*).
N*).①证明:
 ;
;② 求证:
 .
. (Ⅰ)  . (Ⅱ)见解析
. (Ⅱ)见解析
 . (Ⅱ)见解析
. (Ⅱ)见解析本试题主要考查了数列的通项公式的求解和运用。运用 关系式,表示通项公式,然后得到第一问,第二问中利用放缩法得到
关系式,表示通项公式,然后得到第一问,第二问中利用放缩法得到 ,②由于
,②由于 ,
,
所以 利用放缩法,从此得到结论。
利用放缩法,从此得到结论。
解:(Ⅰ)当 时,由
时,由 得
得 . ……2分
. ……2分
若存在 由
由 得
得 ,
,
从而有 ,与
,与 矛盾,所以
矛盾,所以 .
.
从而由 得
得 得
得 . ……6分
. ……6分
(Ⅱ)①证明:
证法一:∵ ∴
∴
∴
∴ .…………10分
.…………10分
证法二: ,下同证法一. ……10分
,下同证法一. ……10分
证法三:(利用对偶式)设 ,
, ,
,
则 .又
.又 ,也即
,也即 ,所以
,所以 ,也即
,也即 ,又因为
,又因为 ,所以
,所以 .即
.即
 ………10分
………10分
证法四:(数学归纳法)①当 时,
时,  ,命题成立;
,命题成立;
②假设 时,命题成立,即
时,命题成立,即 ,
,
则当 时,
时,

 即
即
即
故当 时,命题成立.
时,命题成立.
综上可知,对一切非零自然数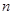 ,不等式②成立. ………………10分
,不等式②成立. ………………10分
②由于 ,
,
所以 ,
,
从而 .
.
也即
 关系式,表示通项公式,然后得到第一问,第二问中利用放缩法得到
关系式,表示通项公式,然后得到第一问,第二问中利用放缩法得到 ,②由于
,②由于 ,
,所以
 利用放缩法,从此得到结论。
利用放缩法,从此得到结论。解:(Ⅰ)当
 时,由
时,由 得
得 . ……2分
. ……2分若存在
 由
由 得
得 ,
,从而有
 ,与
,与 矛盾,所以
矛盾,所以 .
.从而由
 得
得 得
得 . ……6分
. ……6分(Ⅱ)①证明:

证法一:∵
 ∴
∴
∴

∴
 .…………10分
.…………10分证法二:
 ,下同证法一. ……10分
,下同证法一. ……10分证法三:(利用对偶式)设
 ,
, ,
,则
 .又
.又 ,也即
,也即 ,所以
,所以 ,也即
,也即 ,又因为
,又因为 ,所以
,所以 .即
.即 ………10分
………10分证法四:(数学归纳法)①当
 时,
时,  ,命题成立;
,命题成立;②假设
 时,命题成立,即
时,命题成立,即 ,
,则当
 时,
时,

 即
即
即

故当
 时,命题成立.
时,命题成立.综上可知,对一切非零自然数
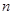 ,不等式②成立. ………………10分
,不等式②成立. ………………10分 ②由于
 ,
,所以
 ,
,从而
 .
.也即


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
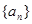 中,
中,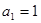 ,
, ,数列
,数列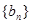 中,
中,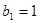 ,且点
,且点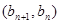 在直线
在直线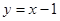 上。
上。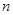 项和
项和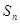 ;
;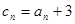 ,求数列
,求数列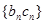 的前
的前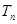 ;
;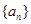 是等差数列,首项
是等差数列,首项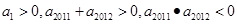 ,则使前n项和
,则使前n项和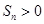 成立的最大自然数n是( )
成立的最大自然数n是( ) 的利润;乙方案:每年贷款1万元,第一年可获利1万元,以后每年比前一年增加5千元;两次方案的使用期都是10年,到期一次性归还本息。若银行两种形式的贷款都按年息5
的利润;乙方案:每年贷款1万元,第一年可获利1万元,以后每年比前一年增加5千元;两次方案的使用期都是10年,到期一次性归还本息。若银行两种形式的贷款都按年息5 的公比
的公比 ,前
,前 项和为
项和为 ,若
,若 ,则
,则 ( )
( )



 的首项
的首项 ,前
,前 项和
项和 .(Ⅰ)求数列
.(Ⅰ)求数列 ,
, ,
, 为数列
为数列 的前
的前 .
.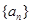 的前n项和为
的前n项和为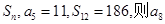 =( )
=( )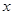 ,
,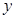 ,3中,前三个数成等比数列,后三个数成等差数列,则
,3中,前三个数成等比数列,后三个数成等差数列,则 = ;
= ;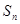 为等差数列
为等差数列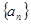 的前
的前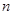 项之和,若
项之和,若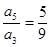 ,则
,则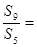 ()
()